La batalla del infinito que terminó con un genio matemático en el sanatorio
Grandes rivalidades de la ciencia
Dos gigantes de las matemáticas, Georg Cantor y Leopold Kronecker, protagonizaron uno de los enfrentamientos científicos más sonados de la Historia. Una pelea repleta de dramas personales y ataques académicos que dio como fruto la teoría de conjuntos
Teller y Oppenheimer: egos, ideología y explosivos
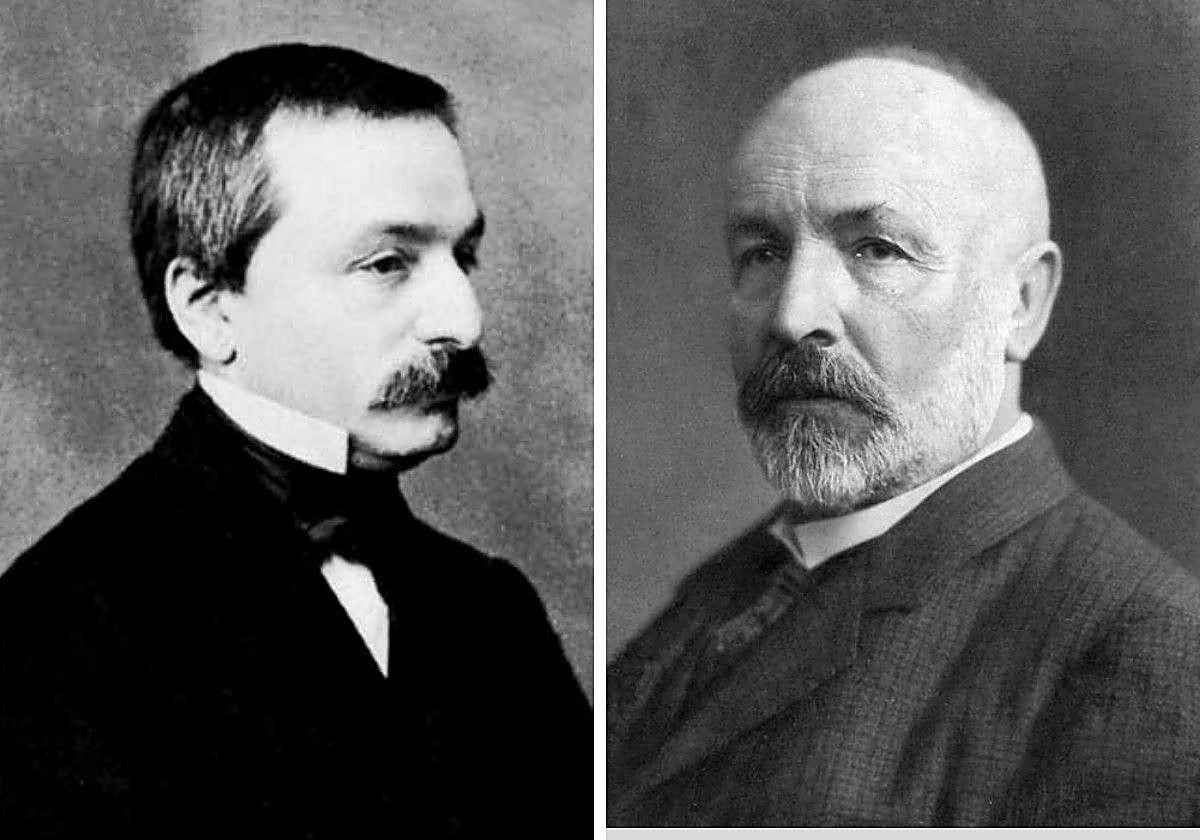

Esta funcionalidad es sólo para registrados
Iniciar sesiónImaginemos por un instante una pelea de titanes donde el campo de batalla son los números, las armas son demostraciones y el botín es, nada menos, que el concepto de infinito. Esto fue precisamente lo que sucedió en el siglo XIX cuando dos gigantes ... de las matemáticas, Georg Cantor y Leopold Kronecker, protagonizaron una de las rivalidades más épicas de la ciencia.
Uno, un visionario que se atrevió a domar el infinito; el otro, un guardián de la ortodoxia matemática dispuesto a tumbar sus ideas. ¿El resultado? Una revolución que cambiaría para siempre el corazón de las matemáticas, acompañada de dramas personales, ataques académicos y una pugna filosófica que aún resuena hoy.
El argumento diagonal de Cantor
Todo comenzó con una pregunta aparentemente simple: ¿puede existir más de un infinito? Cantor, un joven matemático ruso-alemán, creía que sí. Mientras investigaba series trigonométricas, se topó con una idea revolucionaria: los conjuntos infinitos podían tener distintos «tamaños».
Así nació la teoría de conjuntos, donde demostró que los números reales (como pi) eran «más infinitos» que los números naturales (1, 2, 3...). Su arma secreta: el argumento diagonal, un método ingenioso para probar que no podían emparejarse ambos conjuntos.
Fue entonces cuando entró en escena Kronecker, su antiguo mentor y figura dominante en la Universidad de Berlín. Vio allí una herejía matemática. Para él, solo lo «construible paso a paso» era válido. «Dios hizo los enteros; todo lo demás es obra del hombre», proclamaba, rechazando cualquier noción de infinito completo.
El maestro difama al pupilo
La batalla se tornó personal. Kronecker, desde su trono académico, bloqueópublicaciones de Cantor, desacreditó sus ideas en conferencias y hasta disuadió a estudiantes de estudiar su obra.
«¡Corruptor de jóvenes!», le espetó, convencido de que sus teorías llevaban al caos lógico. Cantor, hundido en la depresión y luchando contra crisis nerviosas, escribía cartas desesperadas a colegas: «Kronecker ha convertido mi vida en un infierno».
A pesar de todo, desarrolló los números transfinitos (ℵ₀, ℵ₁...), una aritmética del infinito donde 1 + ℵ₀ = ℵ₀, pero ℵ₀ + 1 era distinto. Era como sumar universos, no manzanas.
La comunidad matemática se dividió. Mientras Kronecker tachaba las ideas de Cantor de «fantasías enfermizas», figuras como David Hilbert las defendían: «Nadie nos expulsará del paraíso que Cantor ha creado».
El conflicto trascendió lo académico: era una guerra entre dos visiones de las matemáticas. ¿Debían basarse solo en objetos finitamente construibles (Kronecker) o aceptar entidades abstractas como conjuntos infinitos (Cantor)? Irónicamente, la resistencia fortaleció a Cantor. Para refutar a sus críticos perfeccionó sus pruebas sentando las bases de la lógica matemática moderna.
El desenlace fue, sin embargo, agridulce. Kronecker murió en 1891 sin aceptar las ideas de su rival. Cantor, aunque reconocido tarde, pasó sus últimos años en un sanatorio, víctima de sus demonios internos. Pero su legado triunfó: hoy, la teoría de conjuntos es el lenguaje universal de las matemáticas.
MÁS INFORMACIÓN
Cada vez que uno de nosotros vea un símbolo de infinito debería recordar esta batalla matemática, porque detrás de ese garabato elegante hay una historia de genio, terquedad y la osadía de pensar lo impensable.
Límite de sesiones alcanzadas
- El acceso al contenido Premium está abierto por cortesía del establecimiento donde te encuentras, pero ahora mismo hay demasiados usuarios conectados a la vez. Por favor, inténtalo pasados unos minutos.
Has superado el límite de sesiones
- Sólo puedes tener tres sesiones iniciadas a la vez. Hemos cerrado la sesión más antigua para que sigas navegando sin límites en el resto.
Esta funcionalidad es sólo para suscriptores
Suscribete
Esta funcionalidad es sólo para registrados
Iniciar sesiónEsta funcionalidad es sólo para suscriptores
Suscribete