Ocho edificios formidables de España con un uso magistral de las matemáticas

No vamos a ser exhaustivos en esta presentación, solo daremos algunas muestras de esta importante relación que, de algún modo, merecen ser destacadas. Comenzaremos por Juan de Herrera : todos hemos estudiado en el colegio que fue el arquitecto del Real Monasterio de San Lorenzo de El Escorial . Si bien las obras de este impresionante monumento comenzaron en 1563 bajo la dirección de Juan Bautista de Toledo , en 1567 Juan de Herrera fue quien se hizo cargo de las obras y fue nombrado arquitecto de l complejo en 1572.

Mientras tanto, seguro que tenía bastantes conversaciones con Felipe II , así que le sugirió la creación de una Academia de Matemáticas y de este modo en 1583 fundó la Academia de Matemáticas y Delineación, de la que además fue su primer director al mismo tiempo que ejercía como “excellente Mathematico y architecto mayor de su magestad”, según consta en el título de su Tratado de la figura cúbica que se conserva en la Biblioteca del Colegio Oficial de Arquitectos de Madrid. Escribió varias otras obras relacionando matemáticas con arquitectura, como un manuscrito sobre la Teoría Matemática de Grúas

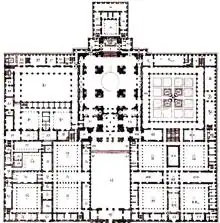
La planta de El Escorial es totalmente geométrica y en ella se aprecia el gusto que Herrera tenía por la forma cúbica: su disposición muestra patios cuadrados.

Dando un gran salto en el tiempo nos situamos 300 años después para descubrir a otro arquitecto que utiliza muchas matemáticas en sus diseños. Antonio Gaudí desarrolla con paraboloides hiperbólicos la cubierta de la cripta de la Colonia Güell , constituyendo así el primer ejemplo de bóveda en la historia de la arquitectura que utiliza estos cuerpos geométricos. No obstante, utilizó esta figura en otras construcciones, culminando con las cubiertas de la Sagrada Familia .

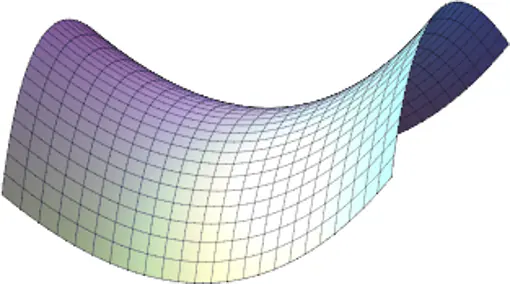
El paraboloide hiperbólico es una superficie que presenta una doble curvatura. Tenemos un ejemplo bastante familiar de esta superficie en la forma de unas conocidas “patatas” fritas. También se conoce al paraboloide hiperbólico como “silla de montar”.

Las construcciones de Gaudí también utilizan hiperboloides y conoides, como en el tejado de las escuelas que se hicieron para los hijos de los trabajadores de la Sagrada Familia , que en la imagen de la derecha aparecen reproducidas con varillas en un trabajo realizado por Inmaculada Conejo para “Matemáticas en la calle” en 2017.

Una idea parecida fue utilizada por Eduardo Torroja para diseñar en 1934 la cubierta de la tribuna del Hipódromo de la Zarzuela , aunque no le parecía demasiado atractivo usar conoides para este cometido y, en sus palabras, “parecía preferible buscar otra superficie de doble curvatura. Entre las formas más conocidas, ninguna parecía tan adaptable como el hiperboloide; por tanto, las bóvedas tomaron la forma de sectores de hiperboloide”. En el año 2009 estas tribunas fueron declaradas Bien de Interés Cultural.

Avanzando hacia nuestros días podemos referirnos a la obra de Félix Candela , quien estudió arquitectura en la Escuela Técnica Superior de Arquitectura de Madrid entre 1927 y 1935. En 1936 se exilió a México, donde trabajó como arquitecto, pero su vida profesional ha estado siempre unida a la docencia: en 1953 obtuvo una cátedra en la Universidad Autónoma de México, desde donde hacía visitas frecuentes a la Universidad de Harvard, hasta que en 1971 comienza a trabajar en la Universidad de Illinois en Chicago. Su última obra la ha dejado en España: él es el autor de L’Oceanografic en Valencia . Esta estructura, que representa un nenúfar sobre el agua, rodea los edificios de la Ciudad de las Artes y las Ciencias y está compuesta por ocho trozos de paraboloide hiperbólico dispuestos de modo simétrico. No pudo terminar su ejecución puesto que Candela falleció en 1997 y el edificio se abrió al público en 2003.

Esta histórica relación entre matemáticas y arquitectura tiene continuidad en la actualidad: del 11 al 13 de julio, en la Escuela Técnica Superior de Arquitectura de la Universidad Politécnica de Madrid se va a desarrollar la Conferencia Internacional “Challenges in Mathematical Arquitecture” donde se abordarán diferentes temas relacionados con el diseño geométrico asistido por ordenador, análisis numérico, modelización matemática en arquitectura, educación de arquitectos y otras aplicaciones y relaciones de las matemáticas con la arquitectura (las personas interesadas pueden inscribirse en este encuentro). La imagen del anuncio del congreso es en realidad la cubierta del patio que hay en el Ayuntamiento de Madrid , en la Plaza de Cibeles. En ella se ve perfectamente la triangulación de la superficie que conforma esta cubierta. A este encuentro asistirán profesionales de los dos ámbitos de conocimiento que se quieren fusionar.

La triangulación permite hacer recubrimientos de diferentes superficies. Hoy es relativamente sencillo hacerlo con software adecuado, de ahí esa necesaria interacción entre matemáticas y arquitectura, pero hace unos años era mucho más complicado puesto que todos los cálculos debían hacerse a mano. Un buen ejemplo donde se aplica este hecho es en la realización de cúpulas geodésicas. La primera fue erigida en 1949 por Buckminster Fuller (otro arquitecto y matemático que merece una sección de ABCdario de las matemáticas para él solo; se la dedicaremos en breve) y en muy poco tiempo comenzaron a levantarse muchas más cúpulas geodésicas.

En España hay varias, pero quizá la más significativa es la que corona el Museo Dalí de Figueras , realizada por Emilio Pérez Piñero . Éste arquitecto había ganado un premio internacional siendo aún estudiante en la ETSAM, pero tras terminar la carrera se dedicó al diseño de diferentes estructuras, culminando con la realización de un pabellón portátil para ferias. Por su parte, Dalí había establecido contacto con Fuller para que acometiera la realización de una cúpula en el Museo de Figueras pero fue el propio Fuller (según las palabras de Dalí) quien le aconsejó que contactase con Pérez Piñero, cuya técnica había avanzado mucho y era capaz de hacer cosas que el mismo Fuller no podía. De este modo fue Pérez Piñero quien diseñó la cúpula, que se construyó entre 1969 y 1972, cubriendo el antiguo escenario del Teatro que ahora alberga a ese museo.

Fernando Blasco es profesor de Matemática Aplicada de la Universidad Politécnica de Madrid, miembro de la Comisión de Educación de la Real Sociedad Matemática Española (RSME) y miembro del Comité de Sensibilización Pública de la Sociedad Matemática Europea.

El ABCdario de las Matemáticas es una sección que surge de la colaboración con la Comisión de Divulgación de la RSME.