Matemáticos encuentran una nueva forma de llegar al número 3

Empezaron encontrando una solución para k = 33, a mediados de septiembre lograron una solución para k = 42 (el único valor que se resistía entre los cien primeros números naturales) y hace unos días han encontrado una nueva solución para k = 3.

569936821221962380720³ + (–569936821113563493509)³ + (–472715493453327032)³ = 3

Ya se conocían dos soluciones para ese valor:

1³ + 1³ + 1³ = 3

4³ + 4³ + (– 5)³ = 3

Aunque los medios sólo mencionan este nuevo hallazgo, lo cierto es que en realidad han sido dos, ya que también han encontrado otro desconocido hasta la fecha

(–74924259395610397)³ + 72054089679353378³ + 35961979615356503³ = 906

Y uno se pregunta, ¿qué aportan esos nuevos casos particulares? Además, teóricamente, ¿no habría infinitas soluciones para cada valor de k?

Aunque hay parte de razón en ese argumento, lo cierto es que el número de soluciones no surge de un modo inmediato, como cabría pensar, por culpa del rápido crecimiento de la potencia tercera. Los valores conocidos eran pequeños, de un solo dígito, pero no hay una solución más hasta números de esa magnitud. Esa es una de las complicaciones. Y encontrar esos valores da pistas sobre cómo localizar más, porque ahora es posible estimar el factor de crecimiento.

La razón de que sea k = 3 el valor en el que se centran las búsquedas no es casual: para k = 1, y k = 2, ya se han encontrado expresiones que dan infinitos valores, para cualquier valor de a y b enteros:

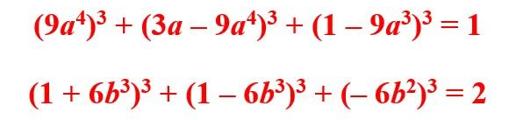
Por otro lado, cuando uno indaga en el modo en que han descubierto esos números (a nadie se le escapa que no debe ser sencillo encontrar valores del orden, dos de veintiún dígitos y uno de dieciocho), y descubre que medio millar de voluntarios se han prestado a utilizar sus ordenadores para hacer los cálculos, cualquiera que no conozca el mundo de la investigación computacional se preguntará, ¿y cuál es el mérito de estos dos señores? Pues evidentemente, el algoritmo empleado.

Cuando uno busca este tipo de soluciones, no lo hace a la fuerza bruta (o sea, probando con todos los números uno a uno), sino que, además de aplicar teoremas y propiedades matemáticas conocidas, experimenta con otras que puedan ser plausibles, y que quizá permitan en un futuro componer una demostración formal correcta. En resumidas cuentas, estos avances, aunque puedan parecer pequeños, insignificantes e inútiles para muchas personas, son necesarios y puede que determinantes a la hora de descubrir otros más relevantes y aplicables. La ciencia avanza a base de pequeños pasitos, pero seguros. Aquí no queda ya espacio ni oportunidad para los descubrimientos por casualidad o hacerse rico y famoso de la noche a la mañana (lamentablemente la idea que esta sociedad transmite a la juventud actual; permítanme que utilice la famosa frase atribuida a James Dean , un poco modificada: vivir deprisa a lo que lleva es a morir joven y no siempre dejar un bonito cadáver).

Como curiosidad, el tiempo que han empleado esos voluntarios en descubrir esos valores, si utilizáramos un único procesador funcionando continuamente, ha sido de cuatro millones de horas, o sea, más de 456 años (espero haber echado bien la cuenta; a mí me salen 456.621 años, considerando 365 días al año). Evidentemente, teniendo en cuenta lo de la obsolescencia programada (que no es legal, pero es comprobable), jamás hubiéramos alcanzado la solución con una única máquina. Por otro lado, las empresas informáticas se pegan literalmente por ser elegidas para llevar a cabo este tipo de trabajos (por algo será; ese sí parece un beneficio tangible e inmediato, siempre que se llegue a algo, claro). En este caso la afortunada ha sido la firma de software Charity Engine para ejecutar un algoritmo.

Conocidas soluciones para todos los valores de k menores que la centena, la búsqueda no ha concluido. El siguiente reto (uno de ellos) es intentar demostrar que existen soluciones para todos los valores de k menores que mil. Sólo quedan nueve casos por resolver: 114, 165, 390, 579, 627, 633, 732, 921 y 975. Si lo intentan, no prueben con valores para x, y, z (en valor absoluto, o sea para valores tanto negativos como positivos), menores que 10^15. Ya está verificado que hasta ese orden de magnitud no existen soluciones.

Alfonso Jesús Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME).

El ABCdario de las Matemáticas es una sección que surge de la colaboración con la Comisión de Divulgación de la RSME.