¿Eres capaz de resolver estos seis problemas de ingenio?

Esta celebración tiene su origen el año 1991, cuando Hubert Curien , ministro francés de Investigación y Tecnología (que había sido también el primer presidente de la Agencia Espacial Europea), abrió los jardines de su ministerio con motivo del décimo aniversario de su creación, bajo el lema “la investigación y la tecnología son tarea de todos”. Al año siguiente creó la “Science en fête” y, sin que sirva de precedente, esta iniciativa ha calado en muchos países quienes, de forma simultánea, reservan una semana para acercar la ciencia a la calle. Un ejemplo: entre el 7 y el 11 de noviembre, se celebra en la Universidad del País Vasco/Euskal Herriko Unibertsitatea la decimoctava edición de la Semana de la Ciencia, Tecnología e Innovación , dedicada a las personas que sientan curiosidad por todo lo que nos rodea y tengan la oportunidad de ver, escuchar, sentir y hablar de ciencia con quienes trabajan en ella.

A pesar de su nombre, las actividades programadas para esta edición no se limitan a una semana, ni siquiera están restringidas al ámbito presencial. Algunas de ellas están abiertas a todos los públicos, de cualquier procedencia. Una de ellas, relacionada con las matemáticas, corresponde al concurso titulado “Problemas con premio” , en el que se propone una colección de problemas de ingenio o lógica, con el fin de promover el pensamiento matemático y estimular el uso de las técnicas de resolución de problemas.

Si quieres participar, encontrarás las bases del concurso en el enlace “Zientzia Astea” pero, si simplemente quieres pasar un rato enfrentándote al reto solitario de resolver los problemas, aquí está la lista con los seis problemas propuestos . Como afirmaba el gran matemático y maestro de docentes George Pólya :

Resolver un problema es encontrar un camino allí donde no se conocía previamente camino alguno, encontrar la forma de salir de una dificultad, de sortear un obstáculo, conseguir el fin deseado, que no se consigue de forma inmediata, utilizando los medios adecuados.

Es muy sencillo comprobar que, si realizamos un corte recto a una tarta, obtenemos dos trozos. Con un segundo corte recto que cruce el anterior, conseguimos cuatro trozos y con un tercer corte recto podemos llegar a siete trozos de tarta.

¿Cuál es el mayor número de trozos que se pueden conseguir con siete cortes rectos? ¿Puedes deducir una regla general?

Expedición: Planeta L. Biólogo: Profesor K. Informe: “El tercer día vimos seres extraños. Aunque tienen veinte dedos en total, como nosotros, tienen una extremidad menos y un dedo más en cada extremidad, lo que les da, por cierto, un aspecto espantoso". ¿Cuántas extremidades poseen dichos seres?

Un conejo lleva una ventaja a un perro que lo persigue equivalente a 50 saltos de conejo. Si un salto del perro equivale a tres saltos del conejo y el conejo da ocho saltos mientras el perro da tres, ¿en cuántos saltos alcanza el perro al conejo?

Una noche oscura hay cinco hombres de este lado del río. Los cinco deben cruzar al otro lado a través de un puente que como máximo puede sostener a dos hombres al mismo tiempo. Tienen una sola linterna. Esto obliga a que si dos hombres cruzan al mismo tiempo, deban hacerlo juntos, a la velocidad del más lento. También obliga a que alguno de ellos vuelva para llevarles la linterna a los que se quedaron. Cada uno tarda un tiempo diferente en cruzar: Genio, veloz como el pensamiento, tarda 1 minuto. Pablo, rápido como su automóvil, tarda 2 minutos. Gustavo, entumecido por los fríos del Polo Norte, tarda 3 minutos. Ángel, que insiste en llevar una caja de cerveza, tarda 4 minutos. Daniel, tullido de una pierna, tarda 5 minutos.

¿Cómo han de realizar los cruces, de uno a otro lado del río, para tardar el mínimo tiempo posible en cruzarlo todos? Calcular también el tiempo mínimo para el caso de n personas.

Ana y Beatriz acaban de hacerse amigas de Carmen, y quieren saber cuándo es su cumpleaños. Carmen no les contesta pero les da una lista de 10 posibles fechas.

15 de mayo - 16 de mayo - 19 de mayo

17 de junio - 18 de junio

14 de julio - 16 de julio

14 de agosto - 15 de agosto - 17 de agosto

Entonces, Carmen les dice al oído, a una de ellas el mes y a otra el día de su cumpleaños, y les pregunta si pueden descubrir la fecha completa. Entonces se desarrolla el siguiente diálogo:

- Ana: No sé cuándo es el cumpleaños de Carmen, pero sí sé que Beatriz tampoco lo sabe.

- Beatriz: Al principio no sabía cuándo era el cumpleaños de Carmen, pero ahora sí lo sé.

- Ana: Entonces yo también sé cuándo es el cumpleaños de Carmen.

¿Cuándo cumple años Carmen?

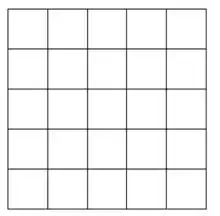
Se dispone de una hoja cuadriculada de tamaño 5x5, como se muestra en la imagen.

Elige uno cualquiera de los cuadrados como punto de partida y desplázate a lo largo de la cuadrícula siguiendo estas reglas:

a. Puedes desplazarte exactamente tres casillas horizontal o verticalmente o bien exactamente dos casillas diagonalmente.

b. No puedes desplazarte a una casilla previamente visitada.

c. No puedes saltar fuera del tablero.

El objetivo es visitar las 25 casillas del tablero. ¿Es posible hacerlo? ¿Cómo? Si no fuera posible, ¿cuáles son el mínimo y máximo número de casillas que puedes visitar siguiendo las reglas indicadas?

A partir del 14 de noviembre, fecha tope para el envío de soluciones, se publicará en esta web la relación de ganadores y las soluciones oficiales de los problemas propuestos.

Pedro Alegría es profesor de la Universidad del País Vasco/Euskal Herriko Unibertsitatea y miembro de la comisión de divulgación de la RSME.

El ABCdario de las Matemáticas es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME).