El puzle que hizo enloquecer a una generación un siglo antes de Rubik

Pues bien, el fenómeno del cubo de Rubik tiene un precedente que se remonta a finales del siglo XIX - el solitario del quince - cuyo recorrido histórico tiene algunas similitudes con aquél y en el que el propio Rubik se inspiró. La historia completa está contada por Jerry Slocum y Dic Sonneveld en el libro “The 15 puzzle”, publicado en 2006.

El puzle del quince es un juego de deslizamiento de piezas que consiste en un cuadrado de 16 casillas que contiene los quince primeros números naturales (pues la casilla que debía ocupar el número 16 está vacía).

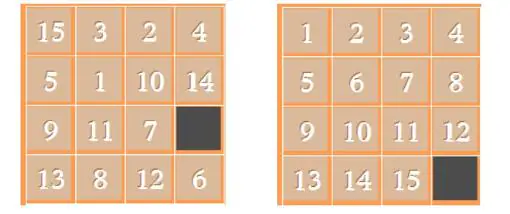
Estas son sus características básicas:

- Cada cuadrado numerado es un bloque deslizante que sólo puede moverse al cuadro vacío.

- Cada movimiento consiste en deslizar un cuadrado numerado sobre el cuadro vacío.

- El objetivo del juego es lograr que las piezas queden colocadas en algún orden predeterminado, por ejemplo colocar las piezas numeradas de menor a mayor, empezando desde arriba y de izquierda a derecha, dejando el hueco en el extremo inferior derecho.

Podemos decir, como primera aproximación, que el cubo de Rubik es una versión tridimensional del puzle del quince.

Sabemos cuál es el origen del juego porque exactamente cien años antes de la patente de Rubik, un funcionario de Correos en Nueva York llamado Noyes Palmer Chapman empezó a fabricar modelos caseros del solitario ahora conocido como el puzle del quince.

A finales de 1879, Matthias Rice, quien dirigía un negocio de carpintería, comercializó el producto bajo el nombre “Gem Puzzle” . Las instrucciones eran muy simples: “Colocar las piezas desordenadamente en la caja para después deslizarlas hasta conseguir ordenarlas de nuevo”.

La propia ambigüedad de las instrucciones y la simplicidad de manejo de las piezas hizo que el juego se convirtiera rápidamente en un fenómeno social. Además, se daba una curiosa circunstancia, nunca vista antes en un puzle:nadie entendía por qué lograba resolver el solitario fácilmente algunas veces y no era capaz de resolverlo otras tantas veces; era relativamente sencillo ordenar las tres primeras filas pero quedaban intercambiados el 14 con el 15.

En 1880, el doctor Charles Pevey ofreció una pequeña recompensa de 100 dólares y una dentadura postiza a quien consiguiera dar con la secuencia de movimientos para llegar a la solución desde el momento en que el 14 y el 15 estaban intercambiados (seguramente porque él mismo afirmaba que la solución es matemáticamente imposible). Bastó este nuevo aliciente para despertar la atención por el juego: se originó una locura colectiva en Estados Unidos la cual se extendió rápidamente por Europa. Ahora bien, de la misma forma que llegó, el interés por el juego se desvaneció: la fiebre remitió rápidamente a mediados de ese mismo año.

Pero no acaba aquí la historia, así como tampoco acabó la del cubo de Rubik cien años después. El prestigioso Sam Loyd (padre), famoso inventor de multitud de juegos y autor de numerosos problemas de ingenio, volvió a resucitar el puzle en 1891. Rápidamente se organizaron concursos y desafíos en relación a este puzle pero los 1000 dólares ofrecidos por Sam Loyd en 1896 a quien primero diera la solución no se entregaron nunca; sin embargo, el interés de la gente dio pie a numerosos episodios anecdóticos que la prensa del momento no dejaba sin reseñar.

Por otra parte, cuando Loyd relanzó el solitario, fue para reclamar su paternidad. Por cierto, sin negar que Sam Loyd fuera el mayor inventor de pasatiempos de la época, es cierto que protagonizó varios conflictos con puzles que él aseguraba –sin tener razón– que eran de su invención (en el artículo de Jerry Slocum titulado 'Sam Loyd’s most successful hoax' se narran las peripecias de algunos de ellos).

Dejando aparte los conflictos personales, veamos qué papel jugaron las matemáticas para justificar que los premios ofrecidos por Charles Pevey y Sam Loyd nunca se entregaran.

En 1879, Woolsey Johnson y William Story , mediante argumentos de paridad en teoría combinatoria, demostraron que no toda posición inicial tiene solución. De hecho, sólo la mitad de los problemas que pueden plantearse tienen solución, independientemente de la estrategia utilizada. Para saber qué configuración inicial tiene solución, basta contar el número de inversiones entre las piezas (alteraciones en su orden natural, sumando el número de la fila del cuadro vacío). Si dicho número es par, pertenece al modelo resoluble I, y si es impar, al irresoluble II.

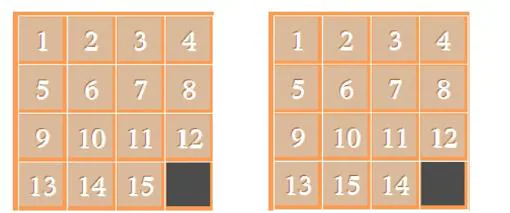
En la figura anterior, la configuración de la izquierda tiene todos los números en el orden natural: el número de inversiones es igual a cero. Como además el cuadro vacío está en la fila cuatro, se trata de una configuración par. Ahora bien, en la configuración de la derecha solo el 15 está invertido con el 14, de modo que el número total de inversiones es igual a uno: se trata del modelo irresoluble.

A pesar de todo, si no se indica que el cuadro en blanco debe quedar en la esquina inferior derecha o que los números estén al derecho, podemos encontrar soluciones ingeniosas que, aparentemente, resuelven el problema pero no como se pretendía. Las que se muestran en la imagen anterior son configuraciones impares.

Actualmente se conocen diversos métodos para resolver el juego del quince y el cubo de Rubik. Sin embargo, a diferencia del solitario del quince, el interés por el cubo de Rubik no ha decaído con el paso del tiempo. Una de las razones es que el algoritmo de resolución del solitario del quince es mucho más sencillo de recordar que el del cubo de Rubik. Pero también es significativa la gran diferencia entre el número total de permutaciones (configuraciones distintas de sus piezas) que se pueden presentar en ambos juegos:

Desde el punto de vista matemático, hay algunas preguntas que todavía pueden plantearse. Por ejemplo, ¿cuál es el menor número de movimientos que son necesarios para resolver alguno de estos solitarios, desde cualquier posición inicial? La respuesta fue dada por Richard Korf en 1985 para el solitario del quince, y en 1997 para el cubo de Rubik. Este valor recibe el nombre de “número de Dios”, y vale 80 para el solitario del quince y 20 para el cubo de Rubik. Incluso, en 2005, el propio Korf estableció el número de movimientos necesarios para cada una de las 1013 disposiciones iniciales del solitario del quince. Por ejemplo, hay 17 disposiciones del tablero que necesitan los 80 movimientos para resolverlo. Es posible descargar el programa que genera todas las soluciones desde la página kociemba.org . En la misma página se afirma que el número mínimo de pasos necesarios para llegar desde la posición natural de las piezas hasta un cuadrado mágico -donde la suma de cada fila, columna y diagonal es igual a 30-, es igual a 35. Además, este caso tiene solución única.

También se han obtenido resultados para la versión del solitario que tiene cinco filas y cinco columnas, con los números del 1 al 24, aunque el número de permutaciones de las piezas es considerablemente mayor que el correspondiente al cubo de Rubik. Estos y otros problemas siguen siendo objeto de estudio de la Inteligencia Artificial , una disciplina que será protagonista en generaciones futuras.

Multitud de variantes del juego, todos con el nombre genérico de rompecabezas de piezas deslizantes, pueden encontrarse en distintos formatos y con gran variedad de diseños. Los más nostálgicos recordarán que el primer modelo de Macintosh llevaba incorporado un programa para jugar al solitario del quince. En la página folklore.org , el propio autor del programa narra sus peripecias.

Pedro Alegría es profesor de matemáticas en la UPV/EHU y miembro de la comisión de divulgación de la RSME.

El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME).