La fórmula que predecía quién ganaba un combate aéreo en la Primera Guerra Mundial

En este modelo se describe la lucha entre dos fuerzas enemigas a través de un sistema de dos ecuaciones diferenciales ordinarias : A’(t) = – ­­b·B(t), B’(t) = – a·A(t). Las variables A(t) y B(t) representan el número de unidades en el instante de tiempo t de los ejércitos alemán (A) y británico (B), y a y b son los respectivos índices de desgaste (es decir, la efectividad que cada una de las fuerzas en contienda tiene a la hora de derribar aviones enemigos).

Grosso modo, cada ecuación nos dice que el número de unidades de cada ejército disminuye de manera proporcional al número de unidades enemigas existentes.

La situación bélica que simula este modelo es aquella en la que las dos fuerzas están formadas por el mismo tipo de unidades y disponen de toda la información táctica posible. Además, cada unidad puede eliminar a una unidad enemiga en cada instante de tiempo de manera que no es posible abatimientos simultáneos. Este es el escenario dominante durante la I Guerra Mundial, tanto en la lucha de trincheras como en las contiendas aéreas (donde el combate cercano o dogfight -lucha de perros, en inglés- era la táctica usual).

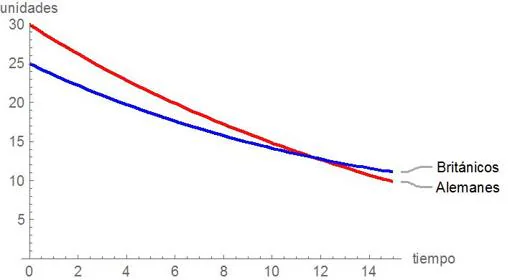
No es difícil comprobar que la expresión en forma implícita de la solución del sistema que gobierna la dinámica del modelo es a·A(t)² - b·B(t)² = a·A(0)² – b·B(0)², donde A(0) y B(0) son los números de unidades de las fuerzas alemanas y británicas al inicio del combate. El análisis de esta solución, conocida como ley cuadrática de Lanchester, nos aporta información valiosa a la hora de iniciar un combate. Por ejemplo que:

-Antes de iniciar el combate, es preferible aumentar el número de unidades de una de las fuerzas que aumentar su efectividad.

-Es posible saber de antemano el resultado de la contienda. Por ejemplo, la fuerza aérea británica acabaría con todos sus oponentes alemanes si entrara en combate con un número de unidades B(0) que verificara la siguiente ecuación: B(0)² > a·A(0)²/b.

-Bajo ciertas condiciones valida teóricamente la estrategia de concentración de todo el esfuerzo bélico en un único punto. Esta técnica, que ya la utilizó Epaminondas en la batalla de Leuctra (371 a.C.) contra los espartanos es formalizada en la teoría del Schwerpunkt o punto focal en la que se basó la Blitzkrieg (guerra relámpago) alemana.

A partir de este primer modelo de combate y basándose en él aparecen sucesivas modificaciones del mismo al considerar distintas situaciones de partida. Así nos podemos encontrar, entre otros, con el modelo logarítmico o el modelo de guerrilla.

En el modelo logarítmico se supone que la disminución de los efectivos de un ejército es proporcional al número de unidades existentes de dicho ejército. Este modelo es especialmente adecuado para simular los primemos instantes de un combate entre fuerzas de tamaño pequeño que se han encontrado por sorpresa y son vulnerables al fuego enemigo. En esta situación, la fuerza con mayor número de unidades es la más vulnerable ya que presenta más objetivos al enemigo.

El modelo de guerrilla se basa en considerar que la disminución del número de unidades es proporcional al producto entre las unidades existentes de ambas fuerzas. Es decir, en este caso el sistema de ecuaciones diferenciales sería el siguiente: A’(t) = - b·A(t)·B(t), B’(t) = -a·A(t)·B(t). Su solución en forma implícita es a·A(t)- b·B(t) = a·A(0) – b·B(0), y recibe el nombre de ley lineal de Lanchester. La situación de combate modelizada por estas ecuaciones es aquella en la que cada unidad es capaz de abatir a todas las unidades enemigas que haya detectado, lo cual es particularmente característico de la guerra de guerrillas en la selva.

Esta familia de modelos de combate de Lanchester ha tenido una gran influencia en el diseño, análisis y toma de decisiones a la hora de plantear campañas bélicas. No obstante, debido a la naturaleza de las técnicas matemáticas empleadas (ecuaciones diferenciales ordinarias), no era posible obtener una simulación espacial del escenario bélico a partir de las mismas. Para evitar esta limitación, se propusieron posteriormente modificaciones de estos modelos basadas en ecuaciones en derivadas parciales que nos proporcionan una predicción espacio-temporal de la dinámica de la contienda.

Ahora bien, todos estos modelos de los que hemos hablado no son capaces de tener en cuenta las características individuales de las diferentes unidades que conforman las distintas fuerzas, ni las interacciones locales entre las mismas. Así, con la finalidad de obtener simulaciones mucho más realistas de los escenarios bélicos, en los últimos años se han empezado a diseñar modelos de naturaleza individual que hacen uso de técnicas íntimamente relacionadas con la Inteligencia Artificial (principalmente modelos basados en autómatas celulares, o modelos basados en agentes).

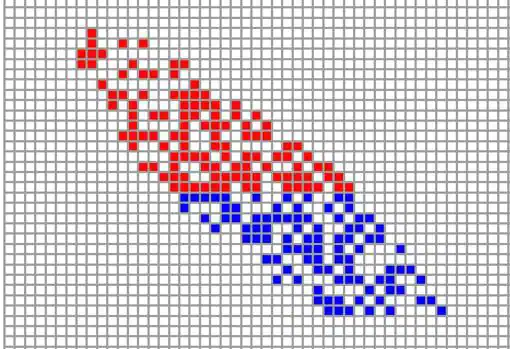
Los autómatas celulares se pueden definir como modelos matemáticos discretos en el tiempo y el espacio caracterizados por la interacción local de los diferentes actores que los constituyen y por la dinámica evolutiva en paralelo de los mismos. Fueron propuestos inicialmente por John Von Neumann y Stanislaw Ulam a mediados del siglo pasado, y popularizados gracias al Juego de la Vida de John Conway y los trabajos teóricos de Stephen Wolfram durante los años ochenta.

Siguiendo este nuevo paradigma, han aparecido recientemente distintos modelos individuales de combate (desarrollados muchos de ellos como fruto de una colaboración entre diferentes agencias gubernamentales y el mundo académico), entre los que podemos citar como los más importantes a MANA (Map Aware Non-uniform Automata), ISAAC (Irreducible Semi-Autonomous Adaptive Combat), y EINSTein (Enhanced ISAAC Neural Simulation Toolkit). En ellos, cada unidad militar individual está caracterizada por parámetros de muy diversa índole (potencia de fuego, capacidad de comunicación, movilidad, moral, etc.) Gracias a ellos es posible obtener simulaciones espacio-temporales tanto a nivel individual como global.

Ángel Martín del Rey es profesor de la Universidad de Salamanca y miembro de la Comisión de Divulgación de la Real Sociedad Matemática Española.

El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME).