Las asombrosas fórmulas matemáticas desarrolladas por un profesor español

Desde pequeño mostró un interés y capacidad para las matemáticas , la mayor parte de las cuales las aprendió por su cuenta, de un modo autodidacta, leyendo los escasos libros que le prestaban. Sin una educación matemática formal, comenzó a escribir fórmulas y resultados en unos cuadernos, que fueron vistos por los matemáticos de algunas instituciones de su entorno para los que resultaban totalmente incomprensibles, ya que se describían sin desarrollo lógico alguno.

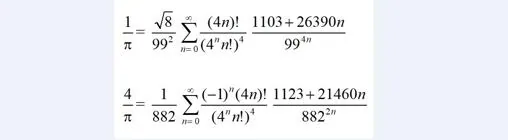
De forma eventual empieza a trabajar como contable en Madrás, trabajo que le resultaba sencillo, lo que le permitía seguir pensando en las matemáticas que él quería. Aconsejado por sus superiores y compañeros decide escribir a matemáticos británicos de relevancia, enviándoles algunas de sus fórmulas y resultados. Muchos no le responden, pero uno de ellos, Godfrey H. Hardy , apoyado por su colega John E. Littlewood quedan profundamente sorprendidos, deseando conocer de primera mano cómo ha llegado a tan sorprendentes expresiones. Y, no sin dificultades, consiguen que Ramanujan se traslade a Inglaterra . Allí, las cosas no serán nada sencillas (estalla además la I Guerra Mundial e Inglaterra queda aislada): no hay demostración alguna de aquellos resultados, y su descubridor sostiene que le fueron revelados por una deidad familiar de la que es devoto. No es difícil imaginar cómo debieron caer tales afirmaciones en un ambiente rigurosamente académico, y cómo debieron sentirse sus valedores. El choque cultural y de divergentes formas de ser no ayudaría al entendimiento.

Lejos de mejorar, las cosas se complicarían por el estado de salud de Ramanujan (enfermo desde niño, vegetariano y sin poder nutrirse adecuadamente con alimentos frescos por culpa del bloqueo), la tensión personal de no estar ni comunicarse con su familia, etc., lo que no debió facilitar su estancia fuera de su país. Tras cinco años en Inglaterra, regresa a su país en 1919, y un año después, fallece a los 32 años . Recientemente se han estrenado dos largometrajes sobre su vida, una coproducción indo-británica de 2014 titulada «Ramanujan» , no estrenada en nuestro país, y «El hombre que conocía el infinito» sobre este singular matemático.

La singularidad de estos trabajos y la peculiar manera de hallarlos, su propia existencia, la dificultad en la comprensión de los apuntes legados en sus cuadernos, han conformado un halo de misterio y romántica leyenda en torno a la figura de este matemático. Una historia única, que tuvo la fortuna de ser conocida, como otras existencias en las más diversas disciplinas (literatura, arte, ciencia, etc.). Seguramente otras muchas hayan tenido lugar a lo largo de la historia, pero no han perdurado.

Salvando las distancias, y las épocas, hay al menos una persona que ha desarrollado fórmulas parecidas (pero diferentes) a las de Ramanujan y que también proporcionan decimales del número π con una notable “velocidad de convergencia”. Entrecomillo esta expresión porque tendríamos que matizarla de forma rigurosa, pero la utilizo porque creo que es la que mejor ilustra lo siguiente: en cada iteración, o sea, en el cálculo de cada nueva aproximación, se añaden (aproximadamente) un número fijo n de cifras decimales correctas. Cuanto mayor sea ese n, más rápida es la convergencia.

Se trata del profesor zaragozano Jesús Guillera (nacido en 1955). Se licenció en Ciencias Físicas en la Universidad de Zaragoza, impartiendo clase en institutos de bachillerato y enseñanza secundaria. En el año 2007 finaliza su tesis sobre artículos que ya le habían publicado, siendo editada en español en formato de libro. Dicha tesis mereció la calificación de Sobresaliente Cum Laude, obteniendo además un Premio Extraordinario. Sus directores fueron la doctora Eva Gallardo Gutiérrez , especialista en espacios de Hardy, y el matemático ruso Wadim Zudilin , que en 2001 recibió, precisamente, el distinguido premio de la sociedad Hardy-Ramanujan. Recientemente, Jesús ha sido nombrado Colaborador Extraordinario del Departamento de Matemáticas de la Universidad de Zaragoza.

El pasado 4 de abril, Jesús fue invitado por el catedrático Doron Zeilberger de la Universidad Rutgers (Nueva Jersey, Estados Unidos) a impartir allí una conferencia.

Zeilberger ha recibido múltiples reconocimientos por sus contribuciones en el desarrollo de la Teoría WZ, que ha revolucionado el trabajo con las series hipergeométricas, entre ellas la medalla Euler (2004) por la utilización de ordenadores y algoritmos en la investigación eficiente de las matemáticas. Es por tanto una gran personalidad en este campo, lo que a su vez prestigia el trabajo y los logros de nuestro compatriota. A su regreso mantuvimos una amigable conversación telefónica y hablamos de su trabajo, entre otros asuntos:

-Cuando uno escucha que no hay explicación a sus fórmulas, pero comprobamos que funcionan, resulta cuanto menos chocante. Es difícil pensar que expresiones tan complejas se hayan obtenido mediante ensayo-prueba-error. ¿Ha sido así en realidad?

-Una de las más recientes ramas de las matemáticas es la que se conoce como “Matemáticas Experimentales”. Su objetivo es desarrollar algoritmos eficientes para descubrir e incluso para demostrar fórmulas, y también naturalmente hacer uso de ellas como si fueran “cajas negras”, es decir, sin que necesitemos saber cómo funcionan internamente. Uno de sus métodos más celebrados son los algoritmos para encontrar relaciones enteras entre ciertas cantidades numéricas. Observando el aspecto de las series de Ramanujan para 1/π pude intuir el aspecto general que debería tener una serie para 1/π^2. Además, resulta que tanto las fórmulas de Ramanujan para 1/π como las mías para 1/π^2 se pueden descomponer en dos y tres series, respectivamente, multiplicadas por ciertos números enteros. Y esos números enteros se pueden descubrir con algoritmos de búsqueda de relaciones enteras y, si son suficientemente pequeños comparados con la precisión numérica con la que operemos, entonces es muy probable que los mismos números enteros sean válidos con independencia de la precisión, y entonces habremos descubierto una fórmula que es muy posible que sea cierta. Una vez descubierta se pueden comprobar muchos más decimales directamente, pero esto tampoco constituye una demostración ya que no hay muchos, sino infinitos. Así que la demostración hay que hacerla con otras técnicas.

- ¿En qué consiste el método Wilf y Zeilberger (WZ)?

- Averiguar la suma exacta de una función g(n) para todos los valores naturales de n suele ser en principio muy difícil. La idea de Wilf y Zeilberger para obtener la suma de ciertos tipos de funciones g(n) consistió en encontrar una función G(n, k) tal que G(n, 0) = g(n) y cuya suma para todos los valores de n fuera independiente del parámetro libre k. Lo que hace el algoritmo WZ es certificar aquellas funciones G(n, k) que tienen esta propiedad, y lo hace hallando una función compañera F(n, k) que nos da la llave de la demostración, y se basa en que el par WZ de funciones (F, G) satisface las siguientes propiedades:

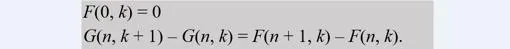
Además el algoritmo está programado para ser usado por ordenador por lo que la función F(n, k) se obtiene de forma automática. Para completar la demostración de una fórmula sólo hay que determinar el valor de esa suma constante y en algunos casos la manera más sencilla de hacerlo es tomando el límite cuando k tiende a infinito. En resumen, lo difícil es descubrir una función G (n, k) adecuada, pero si la encuentras la demostración de la fórmula es automática. Es por ello que hallar pares WZ interesantes es algo muy preciado y por ello suelo decir que son verdaderas joyas matemáticas. Pues bien, utilizando el método WZ he conseguido demostrar hasta ahora cuatro fórmulas para 1/π^2 (dos en el año 2002, otra en 2003 y una más en 2010).

- ¿Cree que podría existir un tipo concreto de series infinitas, entre las que estarían las suyas y las de Ramanujan, que aproximarían π con cada vez más decimales correctos en cada iteración? ¿Se estabilizaría ese orden de precisión en algún momento? ¿Qué avances conoce en este sentido que se hayan hecho?

-Las series de Ramanujan para 1/π son sumas de números racionales (aunque se admite un factor global algebraico), o bien de números irracionales pero algebraicos. Hay 36 series racionales de tipo Ramanujan y la más eficiente es la descubierta por los hermanos Chudnovsky (David y Gregory) en la que cada sumando contribuye con 14 decimales correctos. Pero si consideramos también las series irracionales entonces hay una infinidad de ellas. El problema es que, aunque existen series en las que cada sumando contribuye con un número de decimales tan grande como queramos, estas series no son tan amigables y algunas pueden contener números algebraicos muy complicados e incluso sin expresión en forma de radicales. En lo que se refiere a mis fórmulas hay una diferencia crucial con las de Ramanujan y es que parece que sólo puede haber un número finito de ellas y sólo una irracional.

- A nivel personal, ser citado en publicaciones de tanto prestigio y por investigadores de ese nivel, tiene que constituir una satisfacción impresionante. ¿Le ha cambiado en algo su vida personal unos hallazgos de esta importancia?

- Sí, naturalmente. Además, otros matemáticos encontraron conexiones de mis fórmulas con diversas ramas de las matemáticas, por ejemplo, en Teoría de números, en Geometría algebraica y en Geometría aritmética; en temas tan interesantes como supercongruencias, q-análogos, variedades de Calabi-Yau, motivos hipergeométricos, etc. Sin embargo, no ha habido progreso en lo que se refiere a demostrar mis fórmulas con otros métodos y la mayoría de ellas permanecen sin demostración, aunque nadie duda de que sean correctas.

También yo me he embarcado en el estudio e investigación de la nueva familia de fórmulas desde diversos puntos de vista y continúo trabajando en ello. Un reto importante es entender la nueva familia de forma global. Recientemente he conseguido también avances relacionados con las series alternadas de Ramanujan para 1/π, demostrando algo que se creía imposible: que el grado de las ecuaciones modulares que se requiere para deducir estas fórmulas es mucho menor del que se venía utilizando.

- En los últimos tiempos, hay un interés creciente por conocer las matemáticas (y la ciencia en general) fruto de la cual son tantas publicaciones, páginas web, secciones en prensa tradicional, incluso programas de radio y televisión, etc., en nuestro país (y otros). ¿Qué opina sobre ello? ¿Cree que es una moda pasajera, o realmente piensa que la sociedad se ha empezado a dar cuenta de que estos asuntos tienen interés y futuro?

- La divulgación científica de la Física, Química, Medicina, Genética, etc., resulta atractiva a muchas personas, pero divulgar matemáticas es muy difícil sin incluir fórmulas, y si se incluyen, parece que muchas personas se asustan. Pero bueno, siempre puede haber algunas personas, aunque sean pocas, que aprecien la belleza de las buenas matemáticas y sientan interés en aprender más. Además, hoy hay más medios que nunca debido a la cantidad de información que hay en web y al potente software matemático disponible. Y buenas páginas web enlazan a buenas páginas, pero ¡cuidado!, también hay malas.

- He leído que, en su caso, las matemáticas le sirvieron de un modo terapéutico de válvula de escape y recuperación de la ilusión en unos momentos personales difíciles. ¿Cómo fue acudir a esa opción, y no a la literatura, el cine, en fin, otras menos complicadas? ¿Por qué no la Física, dada su formación? ¿Por qué las matemáticas?

- Para comprobar teorías de la Física hay que hacer experimentos que no se pueden llevar a cabo en casa. Si estudié Físicas es porque un primo mío me regaló un libro de divulgación y quedé fascinado con lo que leí sobre la teoría de la relatividad de Einstein. Pero siempre me he sentido muy atraído por las Matemáticas y además son imprescindibles para entender bien la Física y otras Ciencias. Otra cosa que facilita la investigación en Matemáticas es que sólo se necesita papel, lápiz y un ordenador. En unos momentos difíciles me puse a leer un libro que me había comprado sobre el número π. Pensé que sería entretenido leer todo lo que se sabía sobre este número. Con lo que yo había estudiado en la carrera y también por mi cuenta pude comprender con facilidad casi todas las fórmulas del libro. Pero cuando vi las de Ramanujan me sentí perplejo, quedé impresionado y pensé: ¿Pero de dónde salen estas fórmulas? Son impresionantes y quiero llegar a entenderlas. Como en el libro había buenas direcciones web, pude ir estudiando y aprendiendo todo lo que pensaba que podría servirme para llegar a entender las fórmulas de Ramanujan.

Jesús Guillera también ha desarrollado algoritmos del tipo de los ideados en 1987 por los hermanos Borwein (Jonathan y Peter) , que aproximan el valor de 1/π mediante sucesiones. Son métodos mucho más “potentes” que los del tipo Ramanujan o Chudnovsky porque en este caso el orden de convergencia es mayor: en cada aproximación, el número de dígitos correctos se multiplica (en lugar de sumarse) por un factor. Concretamente, el algoritmo de Borwein es de orden cuártico, es decir, si en la segunda etapa (o iteración), por ejemplo, tenemos ya 7 decimales correctos, en la siguiente se alcanzarían los 28 (salvo quizá el último o los dos últimos debido a posibles errores de redondeo, truncación o simplificación), en la siguiente los 112, y así sucesivamente, lo cual establece una convergencia muy rápida. Lo que logró el profesor Guillera en 2008 es hallar una generalización de ese método. Describimos simplemente en qué consiste: a partir de las sucesiones c_n y d_n siguientes

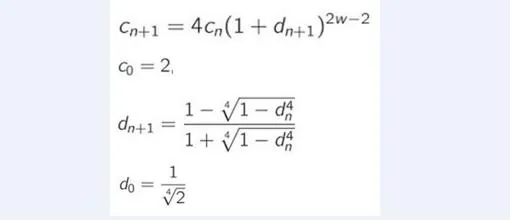
define una tercera, a_n

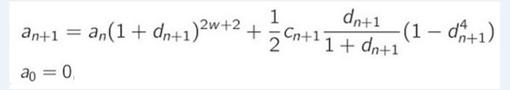
que converge al valor

En el caso particular de w = 1, es el método de Borwein.

A ojos de cualquiera seguramente parezcan expresiones incomprensibles, imposibles de alcanzar. Evidentemente detrás de ellas hay muchas horas de trabajo y estudio, pero como el profesor Guillera ha puesto de manifiesto, perfectamente asequibles, y también en nuestro país. El talento no está limitado por nada. Recordemos que la mayor parte de su trayectoria profesional ha sido como docente en enseñanzas medias, y a este tipo de investigaciones se ha dedicado después de jubilarse, de modo que, además, nunca es tarde para pensar y aportar en matemáticas, echando abajo ese “mito” de que el matemático (y el científico) da todo lo que puede de sí sólo hasta los cuarenta años. Les recomiendo que se acerquen a su detallada página web si quieren conocer más detalles sobre sus trabajos.

Agradezco al profesor Guillera su enorme amabilidad y disponibilidad que me ha permitido compartir con todos ustedes su excepcional trabajo, que ojalá les inspire y anime a seguir su ejemplo.

Alfonso Jesús Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de divulgación de la Real Sociedad Matemática Española (RSME).

El ABCdario de las Matemáticas es una sección que surge de la colaboración con la Comisión de Divulgación de la RSME.