El enigma de los números primos: Del hueso de Ishango al problema del Milenio

En efecto, el hueso de Ishango , un peroné de babuino datado en torno a 20000 a.C., contiene tres columnas de muescas que indican un primitivo sistema de numeración. Se ha señalado el uso de esta herramienta como método de conteo y que sus usuarios dispondrían de algún conocimiento de la multiplicación. También se ha sugerido su uso como calendario lunar de seis meses. En esta pieza, llama poderosamente la atención que la columna de la izquierda muestra los números 11, 13, 17 y 19, es decir, todos los números primos entre 10 y 20; una partición del número 60 (es decir, 11+13+17+19 = 60).

Desde entonces, los números primos fascinarán a generaciones de matemáticos hasta el punto de que diversas escuelas los han dotado de una aureola de misticismo. ¿Pero qué tienen estos números que tanto nos atraen y tanto nos desconciertan? En este artículo trataremos de dar algunas pistas sobre esta cuestión.

Si bien se puede argumentar que los números primos ya aparecen indirectamente en la tablilla mesopotámica Plimpton 322 , datada en torno a 1800 a.C., es en Egipto y más concretamente en el papiro de Rhind (o de Ahmés, si hemos de atenernos a su autoría), donde se muestran de manera más evidente. Datado en torno a 1650 a.C., se trata de un compendio de 87 problemas resueltos de aritmética y geometría. Lo más relevante para nosotros es el tratamiento de las fracciones unitarias (aquellas de la forma 1/n), y en concreto el problema de expresar fracciones del tipo 2/n como suma de dos unitarias. Con admirable destreza, el escriba lo resuelve para los enteros impares entre 4 y 102, salvo en el caso en que n es primo, considerablemente más difícil, y en el que se conforma con expresarlo como suma de tres.

Sobre Pitágoras de Samos (¿569 a.C-475 a.C.?) se ha escrito mucho, aunque él nada escribió, o nada se conserva. Algunos historiadores han cuestionado su existencia, otros creen que realizó numerosos viajes, en particular por Egipto y Babilonia, donde se formó en las matemáticas y el pensamiento de la época.

Se sabe que los pitagóricos manejaban formalmente los números primos; Filolao de Crotona los llamaba números rectilíneos : aquellos que pensados como sucesiones de puntos no se pueden disponer en varias filas del mismo número de puntos cada una. En terminología de la época: número primo es aquél que no se puede medir por ningún otro.

También descubrieron los números perfectos . Un número perfecto es aquel que se puede expresar como suma de sus divisores propios, por ejemplo 6 = 1+2+3 o 28 = 1+2+4+7+14. La relación entre números perfectos y números primos, observada por Pitágoras, pero demostrada por Euclides unos 200 años después es la siguiente:

En el Siglo XVIII, Leonhard Euler demostraría el recíproco de esta afirmación, caracterizando completamente los números perfectos pares en términos de números primos. A día de hoy no se conoce ningún número perfecto impar.

Pero sin duda alguna es Euclides (325 a.C.-265 a.C.) la figura central de la matemática griega, cuyo tratado «Los Elementos» fue la principal fuente bibliográfica en la materia hasta bien entrado el Renacimiento. No examinaremos aquí la enorme relevancia que supone su obra en el pensamiento matemático (en el pensamiento, en general), sino que nos limitaremos a recoger tres de sus resultados sobre números primos. El primero, ya lo hemos mencionado, es el anterior teorema. El segundo, lo estudiamos en nuestra infancia y es la razón de que los números primos merecen ser llamados así, es decir, de que son, en algún sentido, los átomos de los números naturales:

Teorema fundamental de la aritmética (Euclides, Elementos VII, Proposiciones 30 y 31): Todo numero natural mayor que 1 se expresa como producto de números primos de manera única salvo el orden de los factores. Ejemplo:

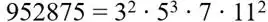
El tercero demuestra la infinitud del conjunto de los números primos y en el lenguaje de Euclides (a los griegos les horrorizaba el infinito; piénsese en las paradojas de Zenón de Elea ) se lee así:

Teorema (Euclides, Elementos, Libro IX, Proposición 60) Los números primos son más que cualquier cantidad dada de ellos.

Demostración: Se prueba por reducción al absurdo, es decir, se supone que lo que se pretende demostrar es falso y mediante una serie de razonamientos válidos se llega a una contradicción, quedando demostrado el enunciado.

Ofrecemos al lector el siguiente problema, de resolución análoga al razonamiento anterior:

Problema: demostrar que existen infinitos números primos de la forma 4n + 3, con n > 0.

Si el lector intenta extender este argumento para probar que existen infinitos primos de la forma 4n+1, se encontrará con un escollo esencial (inténtelo). De hecho, esta cuestión permaneció abierta hasta que Pierre de Fermat , otro gran protagonista de nuestra historia, la resolvió en el S XVII.

Pierre de Fermat (1601-1665), apodado el príncipe de los aficionados, fue un jurista francés que en sus ratos libres se entregaba a las matemáticas y la principal razón por la que ha pasado a la historia es por el enunciado del llamado «Último Teorema de Fermat» , anotado por él mismo en un margen de su ejemplar de la Aritmética de Diofanto , otro de los textos de referencia de la Antigüedad. Sin embargo, aquí solo nos centraremos en sus investigaciones sobre números primos.

Comenzamos por el siguiente resultado, que aparece sin demostración en una carta de Fermat a Frenicle de Blessy fechada en octubre de 1640.

Las cosas pueden incluso complicarse más y darse el caso de que un número compuesto sea pseudoprimo en todas las bases coprimas con él. A tales números se les llama pseudoprimos absolutos o números de Carmichael , de los que el más pequeño resulta ser 561. De estos números no se sabe casi nada, aunque se conjetura que existen infinitos.

El pequeño teorema de Fermat constituye mucho más que una curiosidad: al ser una condición necesaria permite descartar si un número candidato a ser primo lo es en realidad: lo descartamos como primo si no satisface la propiedad. Es decir, es un test de primalidad, algo de enorme interés en criptografía, al ser los números primos la base de diversos criptosistemas. Entre ellos destaca RSA, cimentado sobre una generalización debida a Euler del pequeño teorema de Fermat.

Volviendo a la cuestión de la infinitud del conjunto de primos de la forma 4n+1, ésta se desprende, ahora sí, por reducción al absurdo (dejamos los detalles al lector), del siguiente resultado que Fermat envió por carta a su amigo Marin Mersenne el 25 de diciembre de 1640.

Teorema de Navidad (Fermat). Todo número primo de la forma 4n+1 se expresa de manera única como suma de dos cuadrados perfectos. Así:

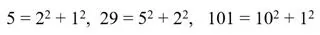
A propósito de Mersenne, debemos mencionar sus números homónimos, de cuyo estudio se ocuparon él y Fermat. Un número de Mersenne es aquél de la forma

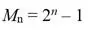
Un poco de reflexión basta para convencerse de que si M_n es primo, hablamos entonces de un primo de Mersenne, entonces n ha de ser primo. Se conocen sólo 51 primos de Mersenne aunque se conjetura, de nuevo, que existen infinitos de ellos. El primo más grande conocido hasta la fecha es de Mersenne; se trata de M_82589933, con 24 millones de cifras.

Además de los números de Mersenne, se tienen los números de Fermat:

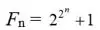
Fermat conjeturó que todos estos números eran primos, pero Euler, nuestro siguiente protagonista, factorizó F_5 = 4294967297 = 641 x 6700417 ya en el S. XVIII. Estos números presentan propiedades notables entre las que destacamos el siguiente resultado:

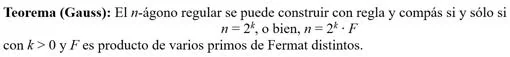
En este vídeo se explica la construcción del heptadecágono (polígono de 17 lados) paso a paso.

Si líneas arriba Euclides nos mostraba que existen infinitos números primos, veamos ahora que, con todo, estos son más escasos a medida que nos alejamos en la recta real.

En primer lugar, existen tramos de números enteros totalmente desprovistos de números primos y de longitud tan grande como se desee; en efecto, para todo n >1, los números n –1 números enteros que hay entre n! + 2 y n! + n son todos compuestos (recordemos que n! = 1.2.3.…n).

En segundo lugar, se puede demostrar que si denotamos por π(n) a la cantidad de números primos menores o iguales que n, el cociente π(n)/n tiende a 0 cuando n se hace grande, es decir, se puede entender que, si se escoge al azar un número entero en un intervalo grande, la probabilidad de que este sea primo resulta despreciable.

En tercer lugar, y ahora es donde no pocos lectores quedarán desconcertados, se tiene:

Teorema (postulado de Bertrand) Para todo n >2, siempre existe algún número primo p entre n y 2n. Por ejemplo, entre 10 y 20 tenemos el 11, entre 15 y 30 el 17, entre 26 y 52 el 29…

También se demuestra lo siguiente:

Teorema (Euler) La serie de los inversos de los números primos es divergente. En concreto, si denotamos por p_n el primo n-ésimo, la suma

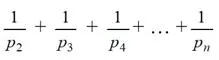
crece arbitrariamente con orden log(log(n)).

Este resultado nos viene a decir que, si bien los números primos son escasos, no lo son tanto como, por ejemplo, los cuadrados perfectos:

En efecto: una serie infinita de términos positivos y que converja ha de estar formada por términos cada vez más y más próximos, lo que equivale a que sus inversos están cada vez más alejados. Los cuadrados perfectos son, en este sentido, más escasos que los primos. ¿No es sorprendente?

Y más aún: al igual que constatamos que existen intervalos de longitud arbitraria desprovistos de números primos, también observamos que hay primos cuya distancia es la mínima posible: 2. A tales primos, como el 5 y el 7, el 11 y el 13 o el 101 y el 103 se les conoce como primos gemelos .

Se conjetura que existen infinitos números primos gemelos . La mayoría de matemáticos creemos que la conjetura es cierta y, por ejemplo, en 1973, Jing Run Chen probó que existen infinitos primos p tales que p+2 es producto de, a lo sumo, dos factores.

Son sólo unos pocos hechos aparentemente contradictorios (sólo aparentemente) que hacen aún más codiciada la búsqueda del santo grial de la aritmética: ¿se puede describir la distribución de los números primos de manera eficiente, o al menos, arrojar algo de luz sobre ella?

En 1737, Leonhard Euler introdujo un objeto que supuso una revolución en el estudio de los números primos; objeto que sería posteriormente generalizado a otros objetos aritméticos, geométricos e incluso analíticos. Hablamos de la función zeta de Euler, definida, para números reales x>1, como:

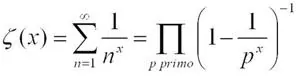
La igualdad de la izquierda define la función, la de la derecha se demuestra usando a) el Teorema Fundamental de la Aritmética y b) la suma de la serie geométrica.

Una primera consecuencia de esta notabilísima igualdad es una nueva demostración, a cañonazos, de la infinitud de los números primos: en efecto, supongamos que sólo hubiese una cantidad finita de ellos; entonces el producto de la derecha sería finito. Pero entonces por la igualdad de la derecha, la expresión de la izquierda estaría definida en x =1; imposible pues la serie de los inversos de todos los números naturales es divergente.

Pero fue Bernhard Riemann (1826-1866) quien explotó en profundidad las propiedades de la función zeta, extendiendo su dominio, es decir su conjunto de definición, a todo el plano complejo salvo x=1. En su memoria de 1859 «Über die Anzahl der Primzahlem unter einer gegebenen Grösse» (Sobre el número de primos menores que una cantidad dada), Riemann usa las propiedades analíticas para expresar diversas transformaciones de la función zeta en términos de funciones aritméticas evaluadas sobre los números primos, formulando la siguiente observación, uno de los problemas matemáticos abiertos más resbaladizos y de solución más codiciada por la comunidad matemática, premiado con un millón de dólares por la fundación Clay :

Conjetura (Hipótesis de Riemann) Todos los zeros no triviales de la función zeta de Riemann tienen parte real igual a 1/2.

Numerosos resultados en teoría de números utilizan propiedades establecidas o conjeturales de la función zeta de Riemann; por ejemplo, Hadamard y De la Vallée-Pousin demostraron independientemente el Teorema de los Números Primos, que grosso modo establece que π(n) se aproxima razonablemente bien por n/log(n), de donde se deriva que el número primo n-ésimo puede aproximarse por nlog(n). Para ello utilizaron que la función zeta de Riemann no tiene zeros en cierta región vertical del semiplano superior. La validez de la hipótesis refinaría resultados ya probados, como el error de esta aproximación, y en suma, arrojaría luz sobre la errática distribución de los números primos.

Iván Blanco Chacón es profesor e investigador en la Universidad de Alcalá de Henares.

El ABCdario de las Matemáticas es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) .