El matemático que propuso cortar un nudo gordiano (y aprender algo en el camino)

Todo aficionado a la matemática recreativa probablemente haya visitado o ido a parar en algún momento a la página educativa Cut the knot (Corta el nudo), y/o a su menos conocido blog hermano CTK Insights , en el que se amplían los contenidos con más aparataje y demostraciones técnicas matemáticas. En ellas podemos encontrar decenas de problemas, acertijos, applets y retos matemáticos de lo más variado.

Su propósito es alentar el interés y provocar la curiosidad por este tipo de desafíos, además de divulgar el papel de las matemáticas en asuntos cotidianos. Esta web ha obtenido más de veinte premios de publicaciones científicas y educativas, incluyendo el prestigioso Scientific American Web Award en 2003 (otorgado por la revista Scientific American, revista insignia de la divulgación científica cuya versión española es Investigación y Ciencia), el Encyclopædia Britannica's Internet Guide Award , y el premio Science's NetWatch. La filosofía de esta página se resume en una frase de su manifiesto: «Un recurso que ayude a aprender, si no matemáticas en sí, que sea capaz, al menos, de mostrar formas de apreciar su belleza».

Aunque no es el motivo de esta reseña, considero pertinente recordar brevemente a qué hace referencia la expresión “Corta el nudo” que da nombre a esta página web. En una de tantas maravillosas leyendas de la Antigüedad, en cierta ocasión los habitantes de Frigia (en la actual Turquía) precisaban elegir rey. A falta de otro procedimiento mejor, casi siempre se nos cuenta que, consultado el oráculo correspondiente (desde luego un buen oficio en aquel tiempo al que muchos listillos en la actualidad intentan seguir sacando partido; habría que analizar los méritos para alcanzar tal honor, antes y ahora), éste indicó que deberían designar a aquel que cruzara una de las puertas de la ciudad acompañado de un cuervo posado sobre su carro. Nunca se nos dice en este tipo de historias si se tardó mucho o poco, o si toda esta parafernalia preparatoria de expectación se hacía a posteriori o no, lo cierto es que, como no hay que defraudar al personal, aparece un buen día un inocente labrador, bastante pobre por cierto (una constante ejemplificadora, presente en muchas de estas leyendas, pero que en la realidad no suele pasar) de nombre Gordías que casualmente cumplió con el requerimiento, y sin comerlo ni beberlo le cayó el papelón encima.

Encantado de la vida, obviamente, ofrece al dios Zeus como agradecimiento su carro, al que ata su lanza y el yugo de sus bueyes con un nudo tan recio que nadie podía desatar, el conocido como nudo gordiano . Y como aquella otra leyenda de la espada en la roca de otro contexto, pero la misma finalidad (¿os dais cuenta que todas las historias legendarias se repiten en distintos lugares simplemente cambiando los protagonistas, adaptándolas ad hoc? Pues todavía hay quien se las cree a pie juntillas), aquel mortal que lograra desatarlo, conquistaría toda Asia. Y llegó por supuesto (lo mismo de antes: no hay que decepcionar al público), un tal Alejandro Magno. Pero éste, bastante bruto a pesar de, se dice, haber tenido unos maestros de primera línea, ni corto ni perezoso, sacó su espada y se cargó el fastidioso nudo por las bravas; y nadie protestó claro, a ver quién se atrevía. Es un claro ejemplo del maquiavélico lema de “el fin justifica los medios”, aunque aquí Alejandro no era tan sutil:

“Da igual cortarlo que desatarlo”. A esta leyenda hace alusión el lema de la página. Además, posteriormente, poniendo un lacito más civilizado a la historia, psicólogos, matemáticos y otros profesionales han adoptado sutilmente la leyenda del nudo gordiano como símbolo del llamado pensamiento lateral: buscar soluciones a los problemas desde enfoques de lo más diversos, inverosímiles incluso, el caso es resolverlo (aunque no sé yo si destruirlo es una solución, pero, en fin, así se contempla).

Sin querer desviarnos más aún del asunto que nos ocupa, pero es que viene bien que en algún momento se nos recuerde de donde parten determinados símbolos con los que a veces nos topamos, habida cuenta de que ya en la escuela no hay tiempo para hacerlo, el católico rey Fernando (el de Isabel; no la serie, sino la reina) hizo suyo este símbolo del yugo con la cuerda cortada, uniéndolo al lema “Tanto monta, monta tanto”, que en origen indicaba eso, que da igual cortar que desatar, aunque después se “apañó” en otro sentido, uniendo como coda a ambos esposos.

Sirva este largo preámbulo como presentación del creador de dicha página web, el matemático y educador ruso Alexander Bogomolny , fallecido el pasado 8 de julio. En su página de Twitter , aún activa, se define como matemático independiente y desarrollador de páginas web educativas, orgulloso estadounidense israelí, con amor y respeto por ambos países. Echemos un rápido vistazo a su trayectoria profesional:

En 1971 se gradúa en matemáticas por la Universidad de Moscú. Se incorpora como investigador al Instituto de Dispositivos de Control Electrónico de Moscú trabajando en métodos numéricos para cálculos en circuitos eléctricos y programación no lineal hasta 1974. Se traslada ese año a Israel, al Laboratorio de Investigación Lake Kinneret, en la ciudad de Tiberíades, como programador y consultor de software, en tareas de análisis armónico de datos y procesamiento de datos numéricos. Paralelamente, en 1976 desarrolla e implementa un proyecto de simulación estocástica sobre el rendimiento y confiabilidad de baterías solares a gran escala para la Universidad Ben-Gurión del Néguev en Beerseba, Israel. Entre 1976 y 1981, prepara su tesis doctoral A New Numerical Solution for the Stamp Problem, dirigida por Gregory I. Eskin, en la Universidad Hebrea de Jerusalén, Israel. Obtiene trabajo como docente en la Universidad Estatal de Ohio y posteriormente, en 1984, en la de Iowa, impartiendo clase como profesor asociado en prácticamente todos los cursos de pregrado de matemáticas. En esa institución pone en marcha e imparte un curso de posgrado sobre los fundamentos matemáticos del diseño de gráficos por computadora y Geometría Digital, además de asignaturas de su especialidad como Análisis Numérico, Solución Numérica de Ecuaciones Diferenciales, en derivadas parciales, análisis de Elementos Finitos, etc.

Compagina su labor docente con la investigación (soluciones numéricas de ecuaciones integrales y desigualdades), y supervisión de tesis de alumnos de posgrado con los que trabaja en el desarrollo e implementación de algoritmos paralelos en computadoras Encore Multimax, así como en demostraciones animadas sobre aplicaciones conformes. Recibió varias becas y subvenciones de organismos como IBM, NSF y la Universidad de Iowa, para desarrollar éstos y otros proyectos. La empresa de marketing directo y multimedia CompuDoc, Inc., de Nueva Jersey le ofrece el cargo de vicepresidente de desarrollo de Software, y nuevos retos profesionales que acepta, como aventurero innato como asimismo se definía, renunciando voluntariamente a su plaza en la universidad en 1990.

Con una amplia trayectoria en programación y diseño de software, a finales de los noventa intensifica sus colaboraciones en medios digitales y en columnas y revistas digitales, tratando de aunar su experiencia tanto como programador, docente e investigador en matemáticas. Crea entonces Cut the knot (con el mismo nombre tiene una columna en la web de la Mathematical Asociation of America entre 2001 y 2004), que no ha parado de crecer desde entonces, necesitando ayuda de colaboradores y teniendo que aceptar finalmente, en contra de sus principios, la presencia de publicidad para financiar el sitio.

Todo el material que aportan él como los lectores, es de libre acceso y consulta.

A Bogomolny le parecía aberrante que se haya convertido en una norma aceptable manifestar públicamente sin ningún pudor la aversión e incomprensión hacia las matemáticas y todo lo que las rodea (les suena, ¿verdad?). Consideraba que una de las causas podría ser la falta de información de la sociedad acerca de la belleza, utilidad e incluso entretenimiento que esta disciplina nos puede proporcionar, y ese fue el motor que lo impulsó a poner en marcha Cut the Knot. Consideraba que “el aprendizaje parte de la curiosidad y otro propósito de este sitio web es servir como recurso hacia cosas sencillas pero curiosas, que tengan relación con las Matemáticas”.

También es reseñable otra frase que aparece en el manifiesto de su web, y que viene al pelo para todos aquellos que siempre se escudan en el “¿Y eso para qué sirve?” después de haberles contado algún resultado o hecho una demostración matemática: «Juzgar las matemáticas por su valor pragmático es como juzgar una sinfonía por el peso de su partitura».

Si visitamos la página de Cut the Knot encontraremos varias secciones (Aritmética, Juegos y rompecabezas matemáticos, Fractales y Caos, Falacias, Juegos Combinatorios, Álgebra, Ilusiones Ópticas, Probabilidad, Magia matemática con ordenador, Combinatoria, Miscelánea Matemática, Geometría, Matemáticas en las Ciencias Sociales, etc.) cada una con muchas (pero muchas, muchas) propuestas (en inglés, of course), y prácticamente todas con applets para trabajar interactivamente (necesario Java VM2; si no se tiene en el ordenador se indica cómo solucionarlo). A modo de ejemplo y homenaje, describo una cuestión geométrica, sencilla de entender, no tan fácil de demostrar rigurosamente.

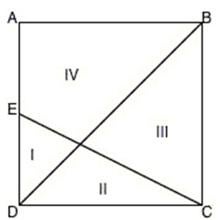
Supongamos que tenemos un cuadrado ABCD como el mostrado en la figura. El punto E es el punto medio del lado AD. Trazamos la diagonal BD y el segmento CE, como aparece en la imagen. Aparecen entonces cuatro regiones etiquetadas como I, II, III y IV. ¿Cómo comparar sus áreas? Dicho de otro modo, establecer un procedimiento para averiguar la proporción entre dichas áreas.

OJO: No se trata de calcular numéricamente el valor de esas áreas, sino de idear un procedimiento para saber la proporción en la que están. Para el que no le guste un enunciado tan “matemático” (a los matemáticos nos sobra la literatura, nos basta lo esencial), piénsese en la parcela que has heredado de algún familiar en la que se han hecho esas partes que vas a alquilar o vender a cuatro personas y deben pagar proporcionalmente a su superficie. Y atento que el catastro no te va a dejar que lo hagas “a ojo de buen cubero” (y tampoco te va a facilitar los datos porque están escasos de personal; la crisis ¿No querían literatura? Pues podemos hasta pergeñar una novela, si es necesario). Se me ocurre que a lo mejor te viene bien recortar un cuadrado en papel y hacer unos dobleces para hacer probaturas y sacar alguna idea, menos radical que la de El Magno.

Y cómo no, a los matemáticos se nos ocurren algunas variaciones: ¿Y si E no es el punto medio, sino que está por ejemplo a 1/3 de AD? ¿Y si en vez de un cuadrado, ABCD es un rectángulo? ¿Se hace igual? Seguro que a ti se te ocurren otras variaciones.

Si después de pensarlo un rato no se te ocurre nada, o quieres comprobar si lo has resuelto bien, pincha aquí y saldrás de dudas.

Alfonso Jesús Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de divulgación de la RSME.

El ABCdario de las Matemáticas es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME).