Por qué crees que has visto una película entera pero en realidad te has perdido la mitad

Nos encontramos ante el típico asunto de proporciones no compatibles , que aparece en más ocasiones de las que creemos en nuestras vidas. Por ejemplo, cuando se estropeó el televisor antiguo de 24 pulgadas que teníamos encajonado en el mueble del salón, y tuvimos que comprar uno de pantalla panorámica porque ya no había otro modelo. ¿Resultado? Era más largo y no cabía. ¿Pero, cómo puede ser, si tiene las mismas pulgadas? Respuesta: porque no tienes ni idea de qué miden esas pulgadas, y aún en el caso de que se supiera, no podían entender que, con el mismo numerito de pulgadas, fuera más largo. Que nos fallan las matemáticas de algo tan sencillo como un rectángulo y por supuesto el teorema de Pitágoras.

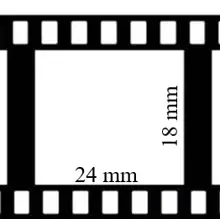
Hagamos un pequeño repaso cronológico. Los primeros aparatos de televisión aparecen en los años cincuenta del siglo pasado en Estados Unidos, Francia e Inglaterra y adoptan las mismas proporciones de las películas de cine de aquel momento, la denotada por 4:3. Esta notación no es más que la relación entre la longitud de la base del rectángulo que constituye la pantalla y la longitud de la altura de la pantalla. A veces se denota también por 1.33:1. La equivalencia es clara: 4/3 es aproximadamente 1.33. Nosotros utilizamos más la notación en forma de fracción; los anglosajones siguen utilizando los dos puntos. ¿Por qué es esta proporción? Porque los fotogramas que componían las películas de aquel momento tenían como medida 24 mm x 18 mm. Si dividimos largo entre alto, tenemos 24/18 = 4/3 = 1.33/1, sin más que dividir la primera fracción entre 6 y la segunda entre 3, respectivamente.

En el colegio nos lo enseñaron, ¿recuerdan? Dos fracciones se llaman equivalentes cuando se multiplican o dividen numerador y denominador por el mismo número. Y dan como resultado el mismo cociente. Así pues, los ingenieros que diseñaron las primeras televisiones emplearon el mismo formato del estándar del fotograma del cine de aquel momento. Hablamos de la película de 35 mm. Que era la más común. Ese valor, 35 mm., resulta al sumar también las perforaciones, es decir, los 18 mm. de alto más la longitud correspondiente a los agujeritos, o sea, la longitud total del fotograma, no sólo lo que se proyecta (el espacio blanco de la imagen anterior).

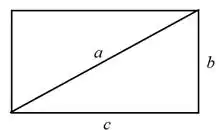
Como recordar dos números parece un trabajo mental «excesivo» (es broma; se hizo por simplicidad), para que quedara definida la televisión que íbamos a comprar a la tienda, se pensó que lo mejor era emplear un único valor. ¿Qué valor determina de manera única el tamaño de un rectángulo? Está claro que lo ideal es saber la base y la altura. Con un solo número, lo lógico es utilizar una longitud que involucre a ambas. Esto se consigue con la longitud de la diagonal del rectángulo, que es la hipotenusa de un triángulo rectángulo. La base y la altura del rectángulo son los catetos de ese triángulo rectángulo, y como todo el mundo ha estudiado el teorema de Pitágoras, a² = b² + c², pues lo tenemos fácil. En el caso del fotograma anterior, a² = 24² + 18² = 900. ¿Cómo despejamos a? Con la raíz cuadrada.

Hete aquí un ejemplo tontorrón donde aparece la raíz cuadrada, para aquellos que siguen con la matraca de ¿para qué se estudia la raíz cuadrada, si no se utiliza nunca? Pues miren, aquí hay que calcular la raíz cuadrada. Que en este caso es muy fácil, se hace a ojo, a = 30 mm., pero en otros casos no, y si no tenemos calculadora, ordenador, móvil, etc., pues hay que hacerla a manopla, con lápiz y papel. Por cierto, aprovechando que el Pisuerga pasa cerquita, si utilizamos la fracción equivalente 4:3, tenemos que a² = 4² + 3² = 25, luego a = 5, que es el 30 anterior dividido por 6. ¿Magia? No, propiedades matemáticas simplemente.

Los países anglosajones acabaron imponiendo su sistema de medidas (lógico porque ellos fueron los que desarrollaron el invento). Y ellos no utilizan los centímetros ni los milímetros, sino las pulgadas. Una pulgada son 2.54 centímetros (o 25.4 milímetros) aproximadamente. Supongamos el triángulo rectángulo de catetos 3 y 4 e hipotenusa 5 que verifica que 3² + 4² = 5² (a la terna (3, 4, 5) por verificar el teorema de Pitágoras se la llama terna pitagórica; esta terna era conocida ya en el antiguo Egipto y se utilizaba para medir ángulos rectos en construcciones, terrenos, etc., con el llamado triángulo de los 12 nudos), Supongamos que 3, 4 y 5 están medidos en pulgadas para hacerlo más sencillo. ¿Cómo conseguimos que la longitud de la diagonal sea 24 (para conocer las dimensiones del televisor de 24 pulgadas)? Se puede resolver mediante una ecuación de segundo grado

(3x)² + (4x)2² = 24²

pero con la propiedad de antes, lo podemos resolver más fácilmente, sencillamente multiplicando la igualdad anterior por el mismo número, (24/5)^2. Haciéndolo, obtendríamos la igualdad

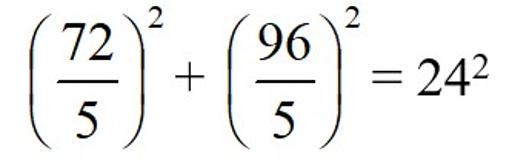
O lo que es lo mismo (14.4)^2 + (19.2)^2 = 24^2. Es decir que el televisor tendrá de pantalla 19.2 pulgadas de largo y 14.4 pulgadas de alto. Para pasarlo a centímetros, basta con multiplicar esos valores por 2.54, lo que nos lleva a que los televisores antiguos de 24 pulgadas tenían una longitud de pantalla de 48.768 centímetros y 36.576 centímetros de altura.

La competencia de la televisión tuvo un gran impacto: la gente dejó de ir a las salas porque podía ver las películas cómodamente en el salón de su casa. Las productoras entonces pensaron en cómo «obligar» al público a volver al cine. Y lo hicieron con la filosofía de dar más que lo que pudiera verse en la pequeña pantalla: cambiaron los formatos de las películas, y aparecieron los formatos panorámicos, que pretendían una amplitud de imagen mucho mayor y unas condiciones de imagen y sonido de una calidad que no pudieran obtener por la tele.

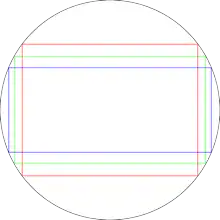
Surgieron muchos formatos. Algunos de los más conocidos son el Cinemascope (con una proporción de fotograma de 2.66:1, también llamada de doble ancho (obsérvese que es exactamente el doble de 1.33), aunque esta proporción se redujo para insertar en los fotogramas la banda sonora quedando finalmente en 2.55:1), el Cinerama (que alcanza los 2.59:1), la Vistavision (se quedaba en 1.5:1, pero mejoraba el grano de la imagen aclarándola y dándole mayor nitidez), etc., hubo muchos más. El tamaño físico de la película se amplió a 70 mm., pero para lograr mayor ancho de imagen, comprimieron las imágenes mediante lentes anamórficas , que luego el proyector de cada sala debía descomprimir según iba proyectando para que se visualizaran de forma natural. A las televisiones las hicieron polvo porque es imposible «meter» un rectángulo de proporciones 16:9 en uno 4:3. En la imagen, el rectángulo rojo es el de la televisión tradicional de 4:3, el verde el del formato 1.85:1 y el azul 2.39:1.

Las televisiones tenían dos opciones: llenar toda su pantalla, mostrando sólo parte de la película (por eso los directores de cine colocaban los pistoleros de un duelo, por ejemplo, de esquina a esquina: si se ve uno, no se ve el otro), una chapuza auténtica, bajo mi punto de vista; o reducir la imagen hasta que quepa toda, introduciendo arriba y abajo unas bandas negras que para algunas personas resultan molestas, pero que es la única manera de ver la imagen de la película completa.

Veamos un ejemplo concreto del efecto. La súper premiada «Ben Hur» (William Wyler, EE. UU., 1959) se rodó con lente anamórfica alcanzando la mayor proporción conocida hasta ese momento (y una de las mayores aún actualmente) 2.76:1. La imagen completa, con sus bandas negras para ver en la televisión es la de la imagen. Corresponde a uno de sus momentos clave, la carrera de cuádrigas . Obsérvese que los protagonistas están en las esquinas. Si queremos llenar todo el televisor, o vemos uno o vemos otro, no hay manera de ver ambos a la vez. En el colmo de la chapuza, surgió un artefacto, llamado pan&scan (palabra compuesta de panorámica y escaneo) que movía la proyección como si fuera un partido de fútbol adonde estuviera la acción. Resultado: muchas veces, cuando un pistolero disparaba y lo veías, cuando la cámara llegaba al otro, llevaba tirado en el suelo media hora (exageración, para que se capte lo que quiero decir). En el caso de Ben Hur, en algún momento, procediendo así, veremos la segunda imagen.

Como vemos, llena el televisor, pero apenas si percibimos la crin de uno de los caballos. Divertido, ¿verdad? Pues así han proyectado la trilogía de Sergio Leone estas Navidades: una sucesión de rostros enormes, piernas sin cabeza en algunos planos, y en el colmo, en el enfrentamiento final de «El bueno, el feo y el malo», nunca, nunca, vimos a los tres personajes enfrentados. Por meter un poco más de leña: proyectarlas así de mal es mucho más barato (la distribuidora no es tonta) que hacerlo bien. La película está rodada en 2.35:1. Los televisores actuales son 1.77:1 (o sea 16:9). Calculen el porcentaje de película se han perdido.

Imaginen cuánto de película se percibe en el caso de «El estrangulador de Boston» (The Boston Strangler, Richard Fleischer, EE. UU., 1968) en la que en determinados momentos suceden cosas simultáneamente en la misma secuencia con hasta ocho ventanas diferentes a la vez. Se rodó en proporción 2.35:1.

Lo dicho, la sala de cine es el sitio en el que se puede disfrutar de la mayor parte de las películas; verlas en la televisión, ordenador, incluso móvil, es simplemente quemar la historia , consumir la película, pero no enterarnos de casi nada de la misma. Cuestión de proporciones.

Alfonso Jesús Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de divulgación de la RSME.

El ABCdario de las Matemáticas es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME).