Así transforman una cara en otra con matemáticas

Aunque hay diversas herramientas matemáticas que pueden utilizarse, probablemente la más fácil de entender sea el uso de triángulos . Para ello, se elige un conjunto de puntos de referencia que permitan caracterizar un rostro; por ejemplo, el punto más alto de la nariz, los extremos izquierdo y derecho de la boca, la barbilla… Una vez encontrados esos puntos en las dos imágenes que queremos fusionar, el siguiente paso consiste en teselar con triángulos ese conjunto de puntos, obteniendo una triangulación.

Ya en 1944, Steward S. Cains demostró que, moviendo adecuadamente los puntos, es posible transformar una triangulación en otra de manera continua.

No obstante, este método pionero tenía una pega, pues necesitaba una cantidad exponencial de pasos para transformar una triangulación en otra. Tuvo que pasar más de medio siglo hasta que, en 1999, Michael S. Floater y Craig Gotsman propusieran un algoritmo alternativo para metamorfosear triangulaciones. Pero este nuevo método también tenía sus inconvenientes, pues solo proporcionaba pasos intermedios, pero no permitía calcular la trayectoria de movimiento de los vértices.

Pero en un artículo publicado recientemente , Alamdari y otros doce autores han conseguido un método que resuelve los inconvenientes de los dos anteriores. Por un lado, es mucho más rápido porque solo necesita una cantidad lineal de pasos, del orden del número de puntos. Por otro lado, sí que permite obtener la trayectoria por la que han de moverse los vértices.

Si te parece, nos vamos a ahorrar los detalles técnicos y solo vamos a echar un vistazo a la idea detrás del método. Esta es bastante sencilla y, esencialmente, la misma que tuvo Cains en el método original.

La técnica, llamada recursión o inducción , consiste en lo siguiente: Si tienes un problema, intenta convertirlo en uno más sencillo y resolver este . A su vez, para este nuevo problema puedes hacer lo mismo, convirtiéndolo en otro aún más sencillo… y así sucesivamente hasta que el problema que te quede sea lo suficientemente sencillo como para conseguir resolverlo. Quizá hasta pueda serte útil en tu vida diaria.

En el problema de metamorfosear triangulaciones, los autores eligen un par de puntos conectados en cada triangulación y mueven uno de ellos hacia el otro. De esa forma el nuevo par de triangulaciones que se obtienen es más sencillo… y van haciendo esto recursivamente hasta llegar a un par de triangulaciones para las que resulte fácil transformar una en la otra.

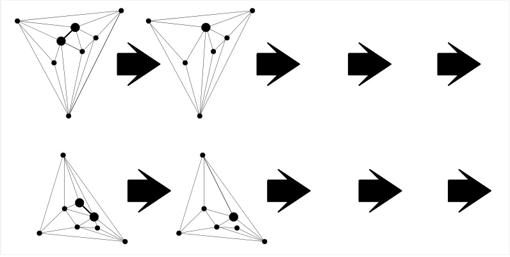
Con esto, la próxima vez que veas una cara transformándose en otra ya te harás una idea de qué es lo que está pasando en realidad. Y, lo que es más importante, ¡sabrás que por debajo hay matemáticas !

David Orden Martín es profesor de la Universidad de Alcalá, miembro de la Comisión de divulgación de la RSME y y del proyecto Marie Skłodowska-Curie 734922 de Horizonte 2020.

El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME).