El teorema matemático para que nadie se quede sin pareja

Por ejemplo, en la disposición de arriba, he encontrado esta solución:

No vayas a pensar que las cartas estaban preparadas porque, a diferencia de la mayoría de solitarios, este no es un juego de azar: sea cual sea el orden de las cartas, siempre existe una solución. Puede que lo difícil sea encontrarla, así que ¡manos a la obra!

¿Te estás preguntando por qué afirmo que siempre existe solución? Esa es la actitud crítica que nos gusta. Allá por el año 1935, el matemático británico Philip Hall probó lo que se conoce como el teorema del matrimonio . Con aquel resultado se resolvió matemáticamente el siguiente problema, hoy en día no tan acuciante:

Dado un conjunto de “m” chicas y “n” chicos, sabiendo que cada chica conoce un determinado número de chicos, ¿bajo qué condiciones es posible que todas las chicas puedan casarse / emparejarse / citarse simultáneamente con uno de los chicos entre sus conocidos?

Philip Hall (1904 – 1982)

El propio enunciado ya obliga a que el número de chicos “n” sea mayor o igual al de chicas “m”. Es fácil encontrar algunos ejemplos sencillos donde no es posible la situación pedida: si dos chicas conocen a un solo chico, y se trata de la misma persona, una de las chicas quedará sin pareja; si tres chicas conocen solo a dos chicos, y son los mismos, tampoco podrán hacerse tres parejas; y así sucesivamente.

Curiosamente, el teorema que demostró Hall asegura que los ejemplos anteriores son los únicos para los que no existe solución. Es decir, si cada conjunto de “k” chicas conoce al menos a “k” chicos, para todos los valores k=1, k=2, …, k=m, entonces es seguro que hay algún emparejamiento posible de todas las chicas con uno de los chicos entre sus conocidos.

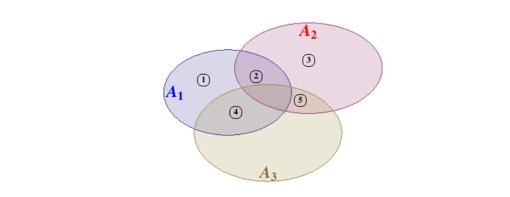
En algunos casos sencillos es fácil representar gráficamente la situación dada: en la primera figura, la chica A1 conoce a los chicos 1, 2 y 4; la chica A2 conoce a los chicos 2, 3 y 5; la chica A3 conoce a los chicos 4 y 5. Un posible emparejamiento, pero no el único, sería (A1, 2), (A2, 3) y (A3, 4).

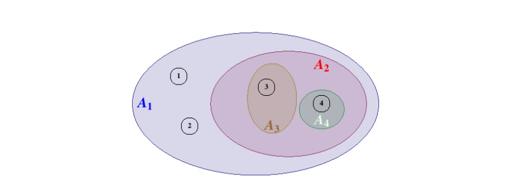
En la segunda figura, la chica A1 conoce a los chicos 1, 2, 3 y 4; la chica A2 conoce a los chicos 3 y 4; la chica A3 conoce al chico 3; la chica A4 conoce al chico 4. Ya no se cumplen las condiciones establecidas por Hall pues se observa que el conjunto formado por las chicas A2, A3, A4 conoce solo a dos chicos. No hay emparejamientos posibles porque las chicas A3 y A4 solo tienen una posible elección, lo cual impide que A2 pueda tener pareja.

La demostración de este resultado se puede encontrar en textos clásicos de Combinatoria y Teoría de Grafos , especialidades matemáticas que requieren grandes dosis de creatividad e ingenio. Por cierto, el teorema no resuelve el problema práctico de encontrar las parejas: solo asegura que hay alguna solución.

Un resultado similar, aunque ligeramente distinto, asegura lo siguiente:

En un grupo de chicos y chicas, si hay algún valor de “k” para el cual cada chico conoce exactamente a “k” chicas y cada chica conoce exactamente a “k” chicos, entonces se puede emparejar a todos los chicos y todas las chicas con alguien (de distinto sexo) a quien conocen.

Evidentemente, el rango de problemas que responden a las características descritas no se reduce al de emparejamiento de seres humanos. El problema de asignar puestos de trabajo a una lista de candidatos, el de elegir campos de cultivo apropiados a diferentes productos, o el de emparejar principios activos con enfermedades concretas, son algunos de los muchos posibles. Si estás interesado, no te será muy difícil encontrar información más completa y detallada en los lugares adecuados, por ejemplo la contenida en el portal brilliant.org.

¡Se me olvidaba! ¿Por qué el solitario planteado al principio tiene siempre solución? Basta imaginar que tenemos 13 chicas –que corresponden a las columnas– y cada una de ellas conoce cuatro chicos –que son los valores de las cartas de su correspondiente columna–. Es muy fácil comprobar que, en dos columnas cualesquiera hay cartas de al menos dos valores distintos, en tres columnas hay al menos tres valores distintos, y así sucesivamente, en “k” columnas hay al menos “k” valores distintos de cartas. Es decir, se cumplen fielmente las condiciones del teorema de Hall.

Termino dejándote una tarea: construye un cuadrado numérico de trece filas y trece columnas asociado al resultado obtenido en el reparto de las cartas. En la primera fila escribe el número de ases que aparecen en cada una de las columnas. En nuestro ejemplo inicial, sería la secuencia

0 0 0 1 0 0 1 0 0 0 0 1 1

En la segunda fila escribe el número de doses, en la tercera el número de treses, y así sucesivamente. Verás que el cuadrado obtenido es casi un cuadrado mágico. ¿Sabes por qué?

El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME).