Hallan una nueva solución al intrigante problema del sofá

«Es un problema sorprendentemente difícil», dice el profesor Dan Romik, presidente del Departamento de Matemáticas de la Universidad de California en Davis (EE.UU.). «Es tan simple que se le puede explicar a un niño en cinco minutos, pero nadie ha encontrado una prueba todavía».

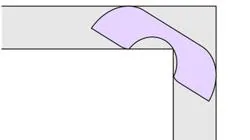
El área más grande que se ajusta alrededor de una esquina se llama la «constante del sofá». Se mide en unidades, donde una unidad corresponde a la anchura del pasillo. El sofá Gerver , que se asemeja a un teléfono antiguo, era el más grande encontrado hasta la fecha que podía pasar por ese pasillo, con una constante de 2,22 unidades, explican en un blog científico de la UC Davis .

Apasionado de la tecnología de impresión 3-D, Romik abordó el problema con la impresora que tiene en su propia casa. «Tener algo que puede moverse con las manos puede ayudar a la intuición», explica el matemático. Y terminó dedicando varios meses al desarrollo de nuevas ecuaciones. «Durante todo ese tiempo no pensé que estaba haciendo investigación. Solo estaba jugando», explica. Pero una idea acudió a su cabeza.

Decidió abordar el problema con una nueva perspectiva, un movimiento ambidiestro. En este escenario, el sofá debe maniobrar tanto a la izquierda como a la derecha 90 grados. Sus hallazgos pueden consultarse online y aparecen publicados en la revista Experimental Matemáticas.

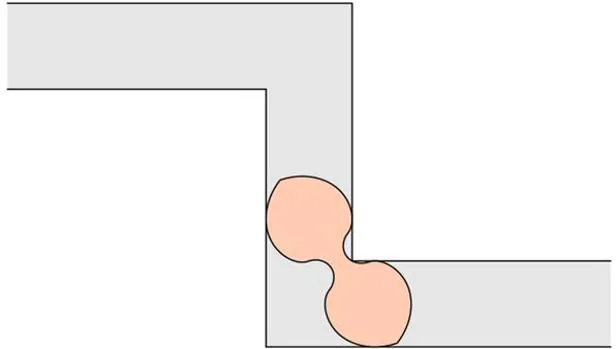
De esta forma, el software de Romik ideó un sofá con una forma semejante a una mancuerna , con curvas simétricas unidas por un centro estrecho. Parece un sujetador sin tirantes. «Recuerdo estar sentado en un café cuando vi esta nueva forma por primera vez», dijo el científico. «Fue un momento muy bonito». El sofá de Romik tiene una constante de 1,64.

Al igual que el sofá Gerver, el sofá ambidiestro de Romik es todavía sólo la mejor conjetura. El problema aún puede conducir a nuevos conocimientos matemáticos, advierte el autor. «A pesar de que el problema del sofá puede parecer abstracto, la solución implica nuevas técnicas matemáticas que pueden allanar el camino a ideas más complejas», dice. «Todavía hay mucho que descubrir en matemáticas».