La hipótesis de Riemann, el más codiciado de los problemas del milenio

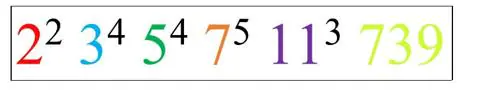
Sin embargo, a diferencia de los compuestos químicos para los que hay una cantidad limitada de elementos básicos (ya sabéis, la tabla periódica), los números primos son infinitos , como demostró Euclides hace unos cuantos siglos (prueba que sigue siendo paradigma de la elegancia, el ingenio y la síntesis, y así seguirá, junto al de la irracionalidad de la raíz cuadrada de 2, ambas aplicando el método de reducción al absurdo , que tanto juego da a la ciencia y que poco se aplica en nuestra vida cotidiana).

Obviamente, al ser piezas básicas, sería deseable conocerlas bien, si fuera posible identificarlas con un golpe de vista, como hacemos con cualquier número divisible por 2, por 3, por 5, etc. Aunque el número tenga decenas de miles de cifras, nos basta con conocer la regla de divisibilidad correspondiente, y aplicarla. Una sencilla receta. Pero con los números primos «nasti de plasti». Qué le vamos a hacer. La vida es dura para todos, también para los matemáticos. Así que, si nos dan un número de, digamos trescientas cifras (nada del otro jueves, por cierto), nos toca empezar a dividirlo por los primos anteriores a él para averiguar si es primo o compuesto. Bueno, no un número cualquiera, un número que acabe en 1, 3, 7 o 9, porque para el resto, el lector sabe que no sería primo a simple vista, ¿no es cierto? Y tampoco hace falta probar con los primos anteriores a él, sino que bastaría con llegar hasta su raíz cuadrada, ¿no? Aun así, esa tarea nos llevaría mucho tiempo, incluso podría agotar la memoria de un ordenador si el número fuera lo suficientemente grande.

Dirán ustedes que «pa qué» tantas cifras, que vaya ganas de perder el tiempo. Razones hay varias, pero seguro que la que más les convence es la de que gracias a números tan grandes y a la imposibilidad hoy por hoy de factorizar números compuestos enormes en un plis plas, a ustedes no les vacían su tarjeta de crédito, no les leen mensajes con información delicada, o les endosan un pufo de esos que últimamente abundan por ahí. Porque entre los sistemas de cifrado que garantizan esa inviolabilidad se encuentran aquellos para los que es imposible por algún motivo determinar la clave a mirones o hackers expertos con ordenadores superpotentes. Y precisamente uno de esos motivos es la dificultad en la factorización de dos números con muchas cifras ( método de clave pública RSA , que a lo mejor un día explicamos con más detalle).

El comportamiento de los números primos parece escapar de cualquier norma razonable, aunque sí se han detectado algunos patrones, que lamentablemente se desvanecen avanzando en la lista. Se han buscado fórmulas (por ejemplo, n2 + n + 41 genera números primos para todos los valores de n en el intervalo [0, 39]; a partir de ahí, se estropea), se han desarrollado algoritmos de factorización y de primalidad , en definitiva, se han generado muchas herramientas (algunas luego útiles en otros contextos), pero no se ha logrado zanjar el asunto para los infinitos primos.

Criba de Eratóstenes : método elemental para encontrar números primos (sólo útil para números no demasiado grandes). A partir del 2 (primer primo) se tachan los números de dos en dos, a partir del 3, de tres en tres, etc., así con todos los múltiplos de cada número primo. Los «supervivientes» (en rosa) son números primos.

Una pauta que se detecta, por ejemplo, es que a medida que los números son más grandes, el número de primos va disminuyendo . Entre 1 y 1000 hay 168 números primos, entre 100000 y 101000 hay 81, pero entre 10^100 y 10^100 +1000 sólo hay 2. Esta progresiva escasez dio pie a pensar en un comportamiento asintótico (en palabras vulgares, que el número de primos se iba estabilizando hacia un valor límite). En ese momento el estudio que había sido con técnicas puramente aritméticas, de teoría de números, cambia al introducir funciones, límites, a intentarse con herramientas de análisis matemático. Se busca una función cuyo comportamiento sea “parecido” al de otra, bautizada como π(x), que indica el número de primos menores o iguales que x. A partir de extensas tablas, Carl F. Gauss en 1798 formula la hipótesis de que para valores grandes de x la función π(x) se comporta como x/ln(x) (ln(x) es el logaritmo neperiano de x; de forma más rigurosa, lo de “se comporta” indica que el límite del cociente de ambas expresiones es 1 cuando x tiende a infinito)

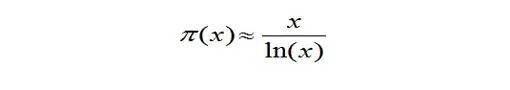
Esta conjetura fue demostrada en 1896 independientemente por dos matemáticos: el francés Jacques Hadamard , y el belga Charles de la Vallée-Poussin , siendo desde entonces conocido el resultado como teorema de los números primos. Unos años antes, en 1838, Gustav Lejeune Dirichlet comunicó a Gauss que había encontrado otra fórmula de aproximación a π(x), expresada como una función integral, que se denominó función logaritmo integral, Li(x)

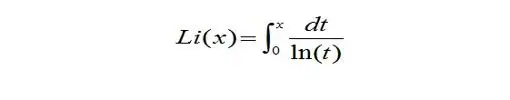
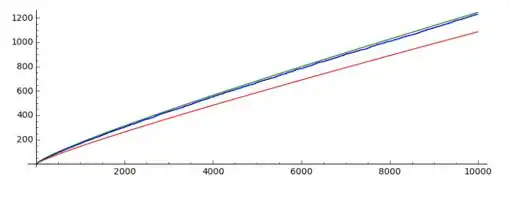
que se comportaba asintóticamente como la de Gauss, pero cuya precisión es sorprendentemente más ajustada a π(x) (recuérdese, el número de primos menores o iguales a x), como se puede ver en la siguiente gráfica

No se crea el lector que estamos escribiendo esto con mucho detalle. Para nada. Es lo más escueto que se puede poner. Entremedias quedan un montón de resultados relacionados con las series numéricas, productos infinitos y otros conceptos matemáticos mucho más técnicos y que exceden con creces el nivel meramente introductorio que pretende esta sección, además de una larga lista de matemáticos que contribuyeron a ir aclarando un poco el terreno (que, por si no ha quedado aún claro, las matemáticas las trabajan personas de carne y hueso, que aunque normalmente no se citan en los libros, los teoremas, nociones y demostraciones, no se han encontrado de la noche a la mañana, ni las ha transmitido un ente misterioso).

En fin, a lo nuestro, que ya vamos llegando a donde queremos. En 1737, Leonhard Euler , describe la siguiente función a partir de una serie numérica (una suma con infinitos sumandos, para entendernos; esa letra sigma grande la llamamos sumatorio y describe esa suma, que empieza en n = 1, como vemos abajo, y acaba en el infinito que se coloca arriba. Si se escribe sin ese símbolo, se van escribiendo los sumandos, terminando en puntos suspensivos queriendo indicar que sigue hasta infinito)

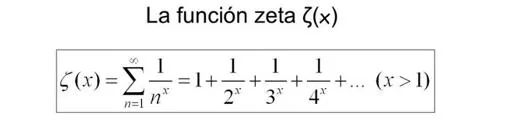
Con esta expresión, Euler demuestra de un modo diferente a Euclides que existen infinitos números primos, pero considera que x sólo toma valores positivos. Otros matemáticos se plantean entonces, ¿y porque no tomar x como número real? Más aún, ¿por qué no considerar que x recorra los números complejos? En este punto es donde aparece Bernhard Riemann , que se percató de que la función zeta puede ser la piedra angular para demostrar el enigma de la distribución de los números primos, después de efectuar sobre ella algunas variaciones.

La función que definió Euler viene expresada por una suma infinita, como vemos y ya hemos advertido. Pero esto no se puede hacer como a uno le venga en gana. Una de las condiciones que hay que cumplir es que esa suma sea un número (técnicamente, que la serie sea convergente). Porque, ¿para qué querríamos una suma que sumara infinito (serie divergente) o no tuviera siquiera suma (serie oscilante)? Si nos fijamos en la imagen anterior, sin hacer mucho ruido, aparece la expresión x > 1. Es decir, la función zeta de Euler tiene sentido únicamente para valores de x mayores que la unidad. Fuera de ese rango no la queremos para nada, porque no es convergente. Para poder extender la función a los números complejos, lo primero que hace Riemann es hacer una prolongación analítica, en un rango en el que la serie compleja sea convergente, «sume algo». Comienza por exigir que los números complejos sean distintos de la unidad, porque para s = 1, la función zeta se hace infinita (es un polo simple). Más aún, comprueba que la función se comporta mucho mejor para números complejos cuya parte real sea mayor que la unidad (matemáticamente se denota mediante Re(s) > 1). Y así obtiene la función zeta de Riemann:

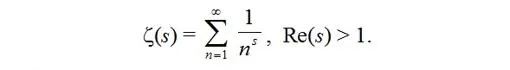
Aclaremos que, para las funciones complejas, hay dos valores que son más importantes que ningún otro, que determinan, junto a alguna otra propiedad, el comportamiento de la función. Son los ceros (los valores que hacen cero la función, aquellos en los que la gráfica corta al eje OX, el de abscisas, el horizontal para entendernos), y los polos (valores para los que la función se hace infinita).

Si representamos gráficamente la función, se observa que tiene un montón de ceros (de hecho infinitos). Riemann se dio cuenta de que existe una relación entre la distribución de los números primos y el número de ceros de la función zeta. Pero no todos los ceros son iguales. Los hay que no aportan información alguna sobre los números primos y aparecen al prolongar la función al plano complejo: son los ceros triviales, que están sobre todos los números enteros pares negativos (−2, −4, −6, …). Nos olvidamos de ellos.

Los ceros que nos importan, los «no triviales», parece que corresponden a números complejos de la forma s = ½ + ib, es decir con parte real ½. Pues esa es justo la hipótesis de Riemann y cuya demostración general está valorada en un millón de dólares: todos los ceros «no triviales» de la función zeta tienen como parte real ½.

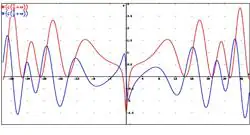
En la imagen aparecen representadas gráficamente la parte real (color rojo) y la parte imaginaria (azul) de la recta crítica Re(s) = 1/2 de la función zeta de Riemann. Pueden verse los primeros ceros no triviales en los valores ±14.135, ±21.022 y ±25.011 (se cortan las líneas azul y roja y el eje OX en esos puntos).

En 1914, G. H. Hardy (el matemático que interpreta Jeremy Irons en la película 'El hombre que conocía el infinito', para los más curiosos) demostró que existe un número infinito de ceros sobre la recta crítica. Sin embargo, podría ocurrir que un número infinito de los ceros no triviales se encontraran en algún otro lugar fuera de la banda crítica. En trabajos posteriores se dieron estimativos para la densidad promedio de los ceros sobre la línea crítica. Otros más recientes se han concentrado en el cálculo explícito de la localización de grandes cantidades de ceros (con la esperanza de hallar algún contraejemplo que refutara la hipótesis de Riemann) y en el establecimiento de cotas superiores en la proporción de ceros que puedan estar lejos de la línea crítica (con la esperanza de reducirlas a cero).

Ni que decir tiene que ha habido muchos investigadores tratando de probar o refutar la conjetura, y se han escrito muchos trabajos (no por el dinero. ¿Ustedes creen que investigaciones de este calibre se pagan con dinero?). Por poner algún ejemplo, en el año 2004 Xavier Gourdon verificó la conjetura de Riemann numéricamente a lo largo de los primeros ¡¡¡diez trillones de ceros no triviales de la función!!! Obviamente esto no sirve como demostración, pero transmite la impresión de que la hipótesis es cierta. Aunque ya saben, mientras no haya una demostración general, no podemos estar seguros.

Si aún quieren más, y desean siquiera constatar los intentos de demostración de la hipótesis desde el año 2000, el matemático Matthew R. Watkins , de la universidad de Exeter (Reino Unido), las ha recopilado en este enlace (algunas son hasta graciosas):

El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME)