El dilema de los cien prisioneros

Como decíamos al principio, este es un problema muy clásico de teoría de juegos y que mucha gente conoce. Hoy les quiero contar un problema menos conocido de prisioneros y dilemas que Alberto Márquez contó hace unos días en nuestro podcast Los 3 Chanchitos : el problema de los 100 prisioneros . Sí, 100, a los matemáticos nos gusta poner a prueba la inteligencia de los reos en situaciones límites.

El problema de los 100 prisioneros fue planteado por Anna Gál y Peter Bro Miltersen , dos investigadores daneses en 2003 y se puede enunciar como sigue:

Tenemos a 100 prisioneros y cada uno de ellos tiene un número distinto (del 1 al 100) en su gorro, que ellos pueden ver perfectamente, basta con que se quiten el gorro. En un habitación de la prisión tenemos 100 casilleros, también numerados del 1 al 100, y dentro de cada cajón hemos puesto una tarjeta con un número del 1 al 100 que, lógicamente, no tiene por qué coincidir con el del cajón en cuestión. El alcaide de la prisión es un poco sádico y les propone jugar para decidir si se salven todos o mueren todos. Para ello, cada prisionero, por separado, entrará en la habitación del casillero, y puede abrir como máximo 50 cajones para encontrar aquella en la que está la tarjeta con el número de su gorro. Antes de salir, vuelve a cerrar todas los cajones. Si, siguiendo estas reglas, todos encuentran su número, se salvan todos. En otro caso, si un prisionero no encuentra su número en las 50 cajones que abre, morirán todos.

¿Con qué probabilidad se salvan todos si abren los 50 cajones a lo loco, sin pensar? Vamos a calcularla, que no es complicado. Para ello pensemos en el primer prisionero: si abre aleatoriamente 50 de los 100 cajones, la mitad, la probabilidad de que encuentre su número es de eso, la mitad, ½.

Si fueran solo dos prisioneros, la probabilidad de que lo encontraran los dos y quedasen libres es el producto de la probabilidades de los dos:

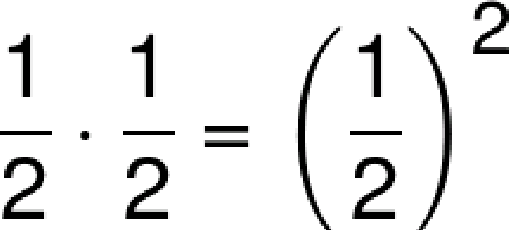
Como son 100 prisioneros, la probabilidad de que todos encontraran su número en estas condiciones sería:

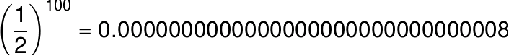
Vamos, que se mueren todos con probabilidad casi del 100%. La crueldad del alcaide es así, qué le vamos a hacer. Bueno, sí que podemos hacer algo. En situaciones desesperadas hay que tomar decisiones desesperadas y en este caso se trata solamente de pensar un poco.

Los prisioneros puede decidir una estrategia ordenada común para todos, al fin y al cabo todos quieren que los demás acierten su número. Y la estrategia es tan simple como la siguiente. El prisionero k (el que lleva una k en su gorro y lo sabe) abre primero el cajón k si está su número, ha ganado; en otro caso, abre el cajón cuyo número ha encontrado en la cajón k. Si está el suyo ha ganado, en otro caso, abre el cajón que indica este segundo número encontrado y así hasta que encuentre el suyo o hasta que haya abierto 50 cajones.

Veamos un ejemplo con 8 prisioneros:

En este ejemplo se salvarían todos. El prisionero 1 abre el cajón 1, después la 3, después la 6 y ahí está su número. Con el resto de prisioneros ocurre lo mismo, encuentra su número antes de abrir 4 cajones

¿Qué pasaría en la siguiente situación?

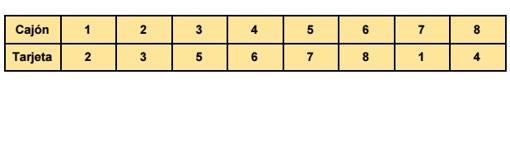
Este es un caso de los chungos porque solo los prisioneros 4, 6 y 8 encontrarían su número con la estrategia y, por lo tanto, morirían todos.

¿Qué diferencia hay entre los dos ejemplos? Vamos a representar ambas situaciones mediante un grafo, que es una herramienta que me encanta y que ayuda en la resolución de un montón de problemas. Un grafo no es más que un conjunto de puntos, vértices, en el que algunas parejas de estos vértices se unen entre sí mediante una línea, arista. Pueden pensar en Facebook como un grafo en el que los vértices son los usuarios y dos vértices estarán unido si son amigos en la citada red social. En realidad, necesitamos un grafo especial, un grafo dirigido porque las aristas serán flechas, con una dirección determinada. O sea, que nuestro grafo se parecerá más a Twitter o Instagram donde el hecho de que un usuario siga a otro no implica que este seguimiento sea mutuo. En nuestro grafo los vértices serán los 8 números y las aristas (flechas) indicarán el recorrido que hace un prisionero por los cajones.

Así, el grafo del primer ejemplo sería el siguiente:

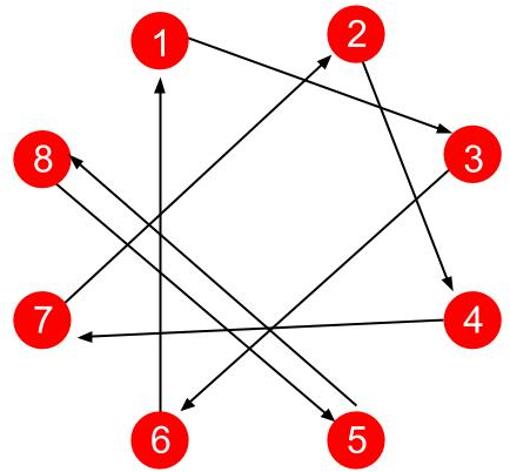
¿Qué observan? Efectivamente, que en esta distribución se forman lo que llamamos en Teoría de Grafos ciclos, caminos circulares de vértices, que son de longitud 3 como máximo, Los hemos coloreado con distintos colores en la siguiente imagen:

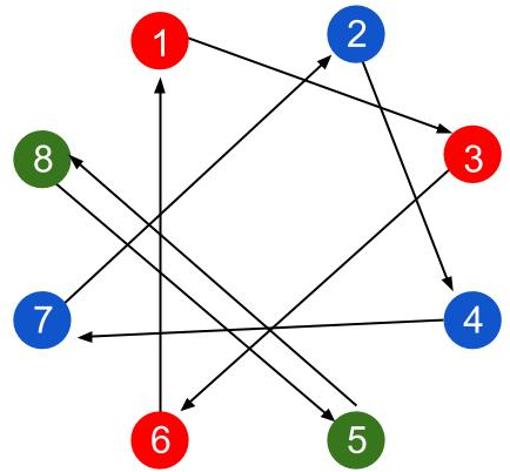
Por lo tanto, ningún prisionero dará más de 3 pasos y no abrirá más de 3 cajones. Porque cualquier camino que empiece en el cajón cuyo número coincide con su gorro regresa a dicho número después de, como máximo, 3 pasos. En el caso del 5 y el 8 solo necesitan 2 pasos.

Sin embargo en el segundo ejemplo, el grafo quedaría así:

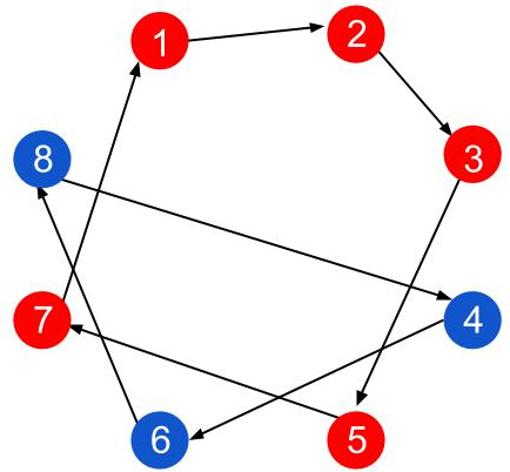
En este caso, según el ciclo en rojo, por ejemplo el prisionero 7 encontraría la tarjeta del 1 en el cajón 7, abriría el cajón 1 y encontraría el 2; abriría el 2 y encontraría el 3; y abriría el 3, y no puede abrir más, y se encuentra el 5. Todos muertos. El problema está en que si el alcaide distribuye los números de esta segunda forma, en el grafo se forma un ciclo de longitud mayor que 4, que son los cajones que puede abrir, la mitad. En este ejemplo, ninguno de los implicados en el ciclo (1,2,3, 5,7) encontraría su número abriendo 4 cajones porque están implicados en un ciclo de longitud 5.

Bueno, esto nos da una pista para calcular la probabilidad de que se salven todos en el caso de 100 prisioneros: la probabilidad de que se salven es la probabilidad de que al hacer la distribución de tarjetas el alcaide, en el grafo dirigido asociado no haya ningún ciclo de longitud mayor que 50. Y esa probabilidad, señoras y señores, es del 0,31183. Dicho de otra manera, la probabilidad de salvarse con la estrategia de abrir los cajones según la tarjeta que contengan es, nada más y nada menos, del 31,18%. Alucinante, ¿no? Recuerden que sin estrategia la probabilidad de salvarse es prácticamente cero. Simplemente, maravilloso.

Y no se puede mejorar, es la estrategia óptima como demostraron Eugene Curtin y Max Warshauer, de la Texas State University-San Marcos, en 2006.

Lo que más me alucina de este problema, aparte de la brillante y óptima estrategia, es que una puede pensar que si el número de prisioneros es muy alto, la probabilidad de salvarse tenderá a 0, será cada vez más pequeña, ¿verdad? Pues no, si el número de prisioneros se hace todo lo grande que una quiera, se hace tender a infinito, la probabilidad de que se salven tiende a 30, 68%. ¿No es maravilloso? Por muchos prisioneros que haya, esta estrategia garantiza la salvación de todos con una probabilidad superior al 30%.

Disfruten del día y no se metan en líos que ya ven cómo se las gastan algunos alcaides.

El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME).